Алгоритмы обхода дерева
Существуют три алгоритма обхода деревьев, которые естественно следуют из самой структуры дерева.
1. Обход слева направо: Left-Root-Right (сначала посещаем левое поддерево, затем – корень и, наконец, правое поддерево).
2. Обход сверху вниз: Root-Left-Right (посещаем корень до поддеревьев).
3. Обход снизу вверх: Left-Right-Root (посещаем корень после поддеревьев).
Интересно проследить результаты этих трех обходов на примере записи формулы в виде дерева, так как они и позволяют получить различные формы записи арифметических выражений.
Пусть для операндов А и В выполняется операция сложения. Привычная форма записи в виде А+В называется инфиксной. Форма записи, в которой знак операции следует перед операндами +АВ, называется префиксной, если же операция записывается после операндов АВ+ – постфиксной.
Рассмотрим небольшой пример, пусть задано выражение А+В*С. Так как умножение имеет более высокий приоритет, то данное выражение можно переписать в виде А+(В*С). Для записи выражения в постфиксной форме сначала преобразуем ту часть выражения, которая вычисляется первой, в результате получим: А+(ВС*).
Теперь запишем в постфиксной форме операцию сложения между операндами А и (ВС*): АВС*+.
Таким образом, выражение А+В*С в постфиксном виде АВС*+, префиксная форма записи будет иметь вид +*АВС.
Рассмотрим различные обходы дерева на примере формулы: ((a+b/c)*(d–e*f )). Дерево формируется по принципу:
– в корне размещаем операцию, которая выполнится последней;
– далее узлы-операции, операнды – листья дерева.
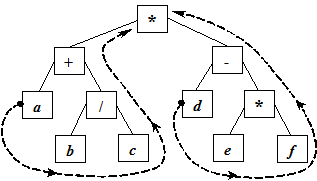
Обход 1 (Left-Root-Right) дает обычную инфиксную запись выражения (без скобок):
a + b / c * d – e * f .
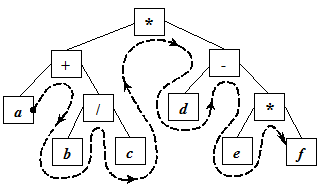
Обход 2 (Root-Left-Right) – префиксную запись выражения (без скобок):
* + a / b c – d * e f .
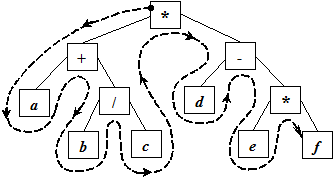
Обход 3 (Left-Right-Root) – постфиксную запись выражения:
a b c / + d e f * – * .
Функция просмотра
Приведем простой пример функции вывода элементов (ключей) дерева, использующий правила обхода 2.
void View ( Tree *t, int level ) {
if ( t ) {
View ( t -> Right , level+1); // Вывод правого поддерева
for ( int i=0; i<level; i++) printf(" ");
printf(“ %d\n”, t -> info);
View( t -> Left , level+1); // Вывод левого поддерева
}
}
Обращение к функции View будет иметь вид View(Root, 0);
Функция View рекурсивная, вторым ее параметром является переменная, определяющая, на каком уровне (level) находится узел. Корень находится на уровне «0». Значения узлов выводятся по горизонтали так, что корень находится слева. Перед значением узла для имитации структуры дерева выводится количество пробелов, пропорциональное уровню узла. Если закомментировать цикл печати пробелов, значения ключей будут выведены просто в столбик.
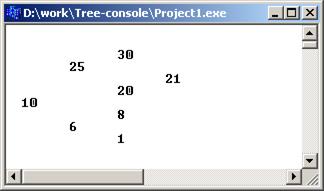
Для последовательно введенных ключей 10 (корень), 25, 20, 6, 21, 8, 1, 30, будет построено дерево, вывод которого на экран с помощью функции View будет иметь следующий вид:
Дата добавления: 2016-01-09; просмотров: 3883;
