Алгоритмы метода Гаусса

Пусть дана система из n линейных алгебраических уравнений с n неизвестными:

(1)

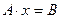
Решением системы (1) называется упорядоченное множество чисел ξ, если подстановка 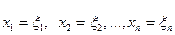превращает уравнения (1) в равенства .

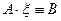Общая схема метода Гаусса для систем, имеющих единственное решение

Пусть 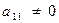. (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на .

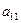Получим

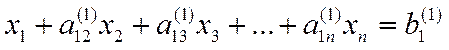, (2)

где ; ,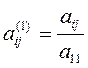

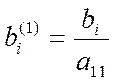
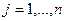
Умножим разрешающее уравнение (2) на 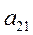и вычтем полученное уравнение из второго уравнения системы (1). Аналогично преобразуем остальные уравнения. Система примет вид

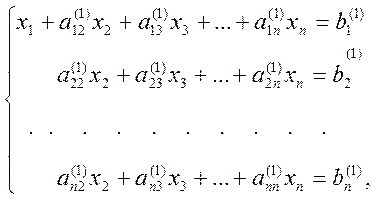(3)

где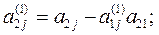

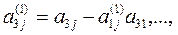
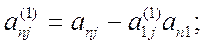
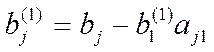
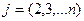
Если какой-либо из коэффициентов 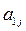окажется равным нулю, то j-ое уравнение системы (1) войдет в систему (3) без изменений т.е.

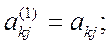
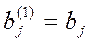
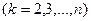
(То есть если в какой-либо из уравнений отсутствовала переменная 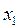, то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая 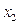из оставшихся уравнений. Получим систему

где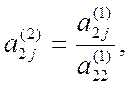

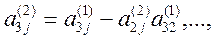
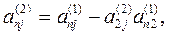
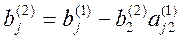
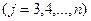
Продолжая аналогичные вычисления, приведем систему (1) к эквивалентной системе с треугольной матрицей коэффициентов

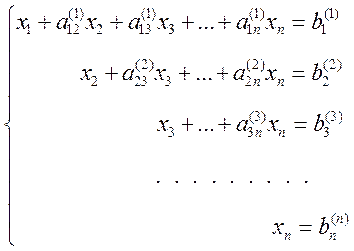(4)

Прямой ход решения выполнен.

Обратный ход:

a) последовательно исключаем неизвестное 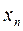, начиная с 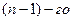уравнения и заканчивая первым. Получаем

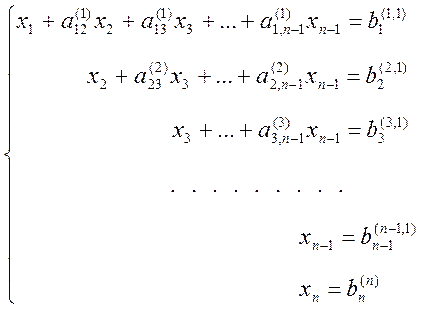(5)

Затем исключаем неизвестное из уравнений с номером j

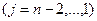и т.д.

В результате получаем решение системы.

Алгоритм Гаусса относится к классу «точных алгоритмов», поскольку можно определить число шагов, необходимых для решения системы линейных уравнений: 2n -1 шаг. Однако числа – приближенные, в силу чего решение задачи также приближенное, а, стало бытьЮ содержит погрешность. При делении на малые помодулю числа погрешность резко возрастает. Для уменьшения этой погрешности применяются модифицированные алгоритмы Гаусса:

- алгоритмы с поиском максимального по модулю элемента по столбцам;

- алгоритмы с поиском максимального по модулю элемента по всей матрице коэффициентов.

При выполнении процедуры прямого хода возможны следующие случаи:

1. матрица А приводится к треугольной (получаю решение).

2. число преобразованных уравнений системы меньше числа неизвестных (ранг матрицы А< n) – Это происходит, если в системе получаются в процессе преобразований тождества 0=0. Система имеет бесконечное множество решений.

3. все коэффициенты при неизвестных в каком-либо уравнении равны нулю, свободный член отличен от нуля. Система не имеет решения.

В случае 3) решение системы может быть найдено приближенно с использованием статистических методов (метод наименьших квадратов (МНК), минимизируюший сумму квадратов «невязок»). МНК широко применяется при обработке измерительной информации.

Случай 2) соответствует недоопределенным системам (системам с неполной матрицей наблюдений), когда число уравнений меньше числа неизвестных. Этот случай весьма часто встречается при анализе технических систем и заслуживает особого рассмотрения.

Задача обработки данных, получаемых в различных технических системах, сводится к нахождению оценок параметров системы, представляющих интерес для исследователя, по имеющимся результатам наблюдений. Пусть

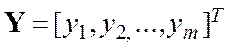- вектор параметров (будем называть его вектором состояния системы) в момент t_j. Z = [z₁, z₂, …z_n]^T - вектор наблюдений, зависящий от вектора Y, т.е.

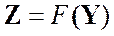(6)

В общем случае зависимость Zот Y – нелинейная, и размерности векторов Zи Yне совпадают. Существуют технические системы, в которых результаты наблюдений являются линейными функциями вектора состояния. Для нелинейных систем зачастую можно применить процедуру линеаризации. При этом уравнение (6) принимает вид

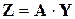,(7)

где А – матрица наблюдений.

При равной размерности векторов Zи Y(m = n) и ранге матрицы А , равном n , имеет единственное решение

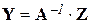(8)

где A^-1– обратная матрица.

Чаще всего имеет место неравенство n > m, т.е. число наблюдений больше числа оцениваемых параметров. В этом случае система линейных уравнений (7) может оказаться несовместной. На самом деле эта несовместность – кажущаяся, т.к. в уравнениях (6) и (7) не учтены погрешности наблюдений – вектор ε , имеющий размерность n. Оценки метода наименьших квадратов – МНК – оценки, минимизирующие сумму квадратов « невязок »ε_i

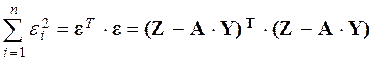(9)

находятся из уравнения [1]

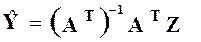(10)

Если ранг матрицы А меньше n , обратной матрицы не существует. В таком случае МНК – оценка вектора Y находится с помощью псевдообратной матрицы А⁺ [2]

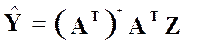(11)

Системы с подобной матрицей – неполной матрицей наблюдений – называют недоопределенными. К таким системам относятся измерительные системы групповых эталонов физических величин, например, эталонов времени и частоты