Общий вид процесса авторегрессии проинтегрированного скользящего среднего. Формы представления модели АРПСС
Целесообразно рассматривать обобщенную форму модели АРПСС, полученную добавлением постоянного члена 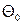 . Запишем в математической формулировке модель авторегрессии — проинтегрированного скользящего среднего
. Запишем в математической формулировке модель авторегрессии — проинтегрированного скользящего среднего
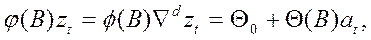 (47)
(47)
где 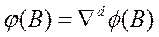 – обобщенный оператор авторегрессии порядка p + d; это
– обобщенный оператор авторегрессии порядка p + d; это
нестационарный оператор, у которого d корней уравнения 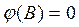 равны единице;
равны единице;
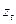 – значение временного ряда в момент t;
– значение временного ряда в момент t;
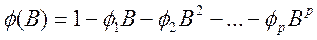 – оператор авторегрессии порядка р;
– оператор авторегрессии порядка р;
предполагается, что этот оператор стационарен, т.е. корни 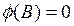 лежат вне единичного круга;
лежат вне единичного круга;
d – порядок разности;
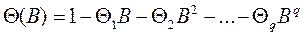 – оператор скользящего среднего поряд-
– оператор скользящего среднего поряд-
у q; предполагается, что он обратим, то есть что корни 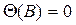 лежат вне единичного круга;
лежат вне единичного круга;
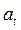 - случайная величина, подчиняющаяся нормальному распределению
- случайная величина, подчиняющаяся нормальному распределению
с нулевым средним и дисперсией 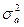 .
.
Когда d = 0 , модель описывает стационарный процесс. Требования стационарности и обратимости накладываются независимо, и в общем случае операторы 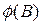 и
и 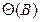 имеют разные порядки.
имеют разные порядки.
Когда постоянный член 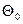 опущен, модель может описывать ряды со стохастическими трендами, например, со случайным уровнем или наклоном ряда. В общем же случае мы можем включить в модель детерминированную функцию времени
опущен, модель может описывать ряды со стохастическими трендами, например, со случайным уровнем или наклоном ряда. В общем же случае мы можем включить в модель детерминированную функцию времени 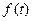 . В частности, автоматический учет детерминированного полиномиального тренда степени d обеспечивается условием, что
. В частности, автоматический учет детерминированного полиномиального тренда степени d обеспечивается условием, что 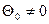 . Например, когда d = 1 , мы можем использовать модель с
. Например, когда d = 1 , мы можем использовать модель с 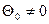 для оценок возможного детерминированного линейного тренда в присутствии нестационарного шума. Поскольку условие
для оценок возможного детерминированного линейного тренда в присутствии нестационарного шума. Поскольку условие 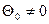 эквивалентно условию
эквивалентно условию
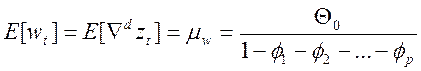 (48)
(48)
не равно нулю, другой способ описания этой более общей модели (3.19) осуществляется в виде стационарного обратимого процесса АРСС, в котором
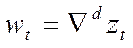 и
и 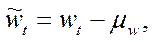 (3.21)
(3.21)
то есть 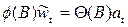 . В тех случаях, когда нет физических причин для существования детерминированной компоненты, среднее значение w может
. В тех случаях, когда нет физических причин для существования детерминированной компоненты, среднее значение w может
предполагаться нулевым, если только это не противоречит данным. Ниже, в
случаях, когда d > 0, мы часто будем полагать, что 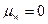 , или, что эквивалентно,
, или, что эквивалентно, 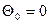 , если только сами данные или смысл задачи не будут указывать на необходимость учета ненулевого среднего.
, если только сами данные или смысл задачи не будут указывать на необходимость учета ненулевого среднего.
Существует три формы представления общей модели АРПСС. Каждая из них имеет свои достоинства и недостатки. Текущее значение 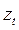 , процесса можно выразить:
, процесса можно выразить:
· через предыдущие значения z и текущее и предшествующие значения а; это достигается прямым использованием разностного уравнения;
· только через текущий и предшествующие импульсы 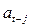 ;
;
· через взвешенную сумму предшествующих значений 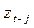 процесса и
процесса и
текущий импульс 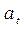 .
.
Здесь рассматриваются стационарно-разностные модели, у которых 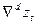 – стационарный процесс и d > 0. Для таких моделей можно без потери общности и опустить
– стационарный процесс и d > 0. Для таких моделей можно без потери общности и опустить 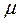 , или, что тоже самое, заменить
, или, что тоже самое, заменить 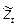 на
на 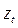 . Эти результаты применимы и к стационарным моделям, у которых d = 0 при условии, что
. Эти результаты применимы и к стационарным моделям, у которых d = 0 при условии, что 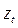 , интерпретируется как отклонение от среднего
, интерпретируется как отклонение от среднего 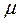 .
.
Прямое использование разностного уравнения позволяет нам выразить теуще значение 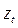 процесса через предшествующие значения z и текущее или предшествующие значения а, Так, если
процесса через предшествующие значения z и текущее или предшествующие значения а, Так, если
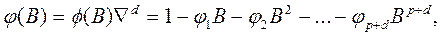 (49)
(49)
общая модель может быть записана в виде
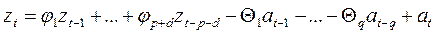 (50)
(50)
Вторая форма представления модели использует случайные импульсы.
При этом линейная модель может быть представлена как выход линейного фильтра
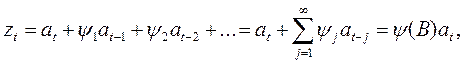 (51)
(51)
входом которого является «белый шум» или последовательность некоррелированных импульсов 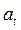 . Иногда полезно представлять модель АРПСС в такой форме. В частности, веса
. Иногда полезно представлять модель АРПСС в такой форме. В частности, веса 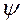 используются для вычисления доверительных интервалов прогнозов.
используются для вычисления доверительных интервалов прогнозов.
Веса 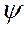 процесса АРПСС можно получить прямо из представления модели в виде разностного уравнения. Общее выражение для весов
процесса АРПСС можно получить прямо из представления модели в виде разностного уравнения. Общее выражение для весов 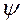 :
:
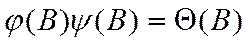 (52)
(52)
Следовательно, веса 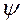 можно получить, приравнивая коэффициенты при одинаковых степенях В в уравнении
можно получить, приравнивая коэффициенты при одинаковых степенях В в уравнении
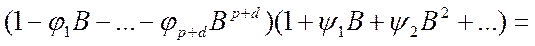 (53)
(53)
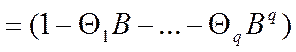
Третья форма описания процессов АРПСС использует обращенное представление модели. То есть модель, выражающую 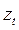 через
через 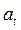 и предшествующие z.
и предшествующие z.
Модель 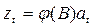 в обращенной форме имеет вид:
в обращенной форме имеет вид: 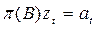 , где
, где 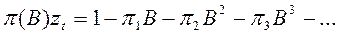 . Здесь
. Здесь 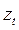 равно бесконечной взвешенной сумме предыдущих значений z плюс случайный импульс, т.е.
равно бесконечной взвешенной сумме предыдущих значений z плюс случайный импульс, т.е. 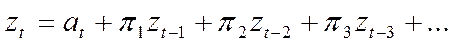 .
.
Веса 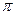 выводятся из разностного уравнения и прямой модели, описанной выше, с помощью таких соотношений:
выводятся из разностного уравнения и прямой модели, описанной выше, с помощью таких соотношений:
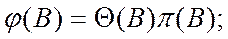 (54)
(54)
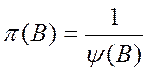
Или в развернутом виде:
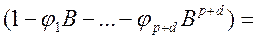 (55)
(55)
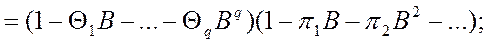

Дата добавления: 2016-02-09; просмотров: 1021;
