Лабораторная работа №2. Анализ остатков от прогнозов
Цель работы: Освоение процедуры проверки гипотез о принадлежности остатков от прогнозов нормальному распределению(Интерактивное обучение -150 минут)
Для правильно построенных (адекватных) моделей остатки от прогнозов должны подчиняться нормальному распределению.
. Однако это предположение не всегда верно. Поэтому необходима проверка гипотезы о принадлежности случайной величины нормальному распределению.
Качественные методы проверки этой гипотезы основаны на сравнении статистической функции распределения с теоретической кривой. Для этой же цели применяются оценки моментов высших порядков:
- коэффициента ассиметрии;
- коэффициента эксцесса,
сравнивается логорифм статистической функции распределения с прямой линией и т. д.
Чтобы получить какую-либо количественную оценку отклонения эмпирического распределения от теоретического ( не обязательно нормального) следует ввести некоторую меру отклонения и затем проверить гипотезу: значимо ли отличается вычисленное значение меры ( для конкретной выборки) от нуля.
Рассмотрим дискретную случайную величину Х,принимающую значения: х1 , х2 , …,хк .
Пусть проведено n независимых опытов. На основе этих опытов составлен статистический ряд распределения случайной величины Х :
| Х1 | Х2 | . . . | Хi | . . . | Хk |
| P1* | P2* | . . . | Pi* | . . . | Pk* |
Где Pi* = ni / n – частота события 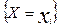 , ni –число опытов, в которых появилось это событие.
, ni –число опытов, в которых появилось это событие.
Выдвигаем гипотезу H0 :случайная величина Х имеет ряд распределений
| Х1 | Х2 | . . . | Хi | . . . | Хk |
| P1 | P2 | . . . | Pi | . . . | Pk |
Отклонение ( Pi*- Pi) вызвано случайными причинами.
Выбираем меру Rрасхождения между гипотетическим распределением и статистическим

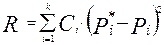
Коэффициенты Сi – веса, учитывающие вклад каждого из отклонений.
При больших вероятностях Рi отклонения ( Pi*- Pi) также будут большими, при малых – малыми. Чтобы уравнять вклады отклонений в сумму, следует взять веса обратно пропорциональными вероятности.
К. Пирсон показал, что, если положить Ci = n /pi то при большом n закон распределения величины Rобладает следующими свойствами:
1. он не зависит от закона распределения случайной величины Х;
2. он мало зависит от n;
3. он при увеличении n приближается к распределению c2 , т.е.
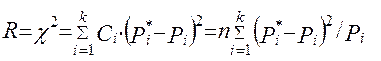 (1)
(1)
Внесем n под знак суммы. Учитывая, что 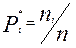 ( ni число значений в i – м разряде),
( ni число значений в i – м разряде),
Получим 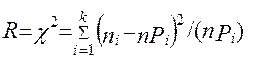 (2)
(2)
c2 – распределение зависит от числа степеней свободы – r.
R = k – l , l – число связей.
Если мы сравниваем наш статистический ряд с гипотетическим распределением, параметры которого известны, то , l = 1, так как наложено одно ограничение
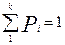 .
.
Если параметры распределения оцениваются по выборке, то l = 1+ q , где q - число оцениваемых параметров.
Вычислив R – статистику и выбрав уровень значимости a , процедуру проверки гипотезы можно применить к проверке соответствия закона распределения некоторому гипотетическому распределению.
Для непрерывных случайных величин Х критерий согласия c2 можно применить, группитуя полученный статистический ряд и заменяя непрерывную случайную величину Х дискретной со значениями 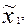
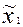 ,
, 
 , где
, где 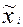 - середина i – го разряда.
- середина i – го разряда.
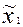
| 
| . . . | 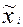
| . . . | 
|
| P1* | P2* | . . . | Pi* | . . . | Pk* |
Рi* - частота попадания в I – ый разряд. 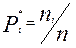 .
.
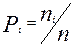
Задание на работу
1. Сгенерировать выборку “ остатков от прогнозов” , считая , что они подчиняются нормальному распределению. ( Объем выборки N и СКО -s заданы в таблице, математическое ожидание m равно нулю).
2. Получить МНК- оценки математического ожидания и дисперсии .
3. Проверить гипотезу о равенстве полученных оценок параметров распределения заданным значениям.
4. При заданных уровнях значимости a1= 0,1 и a2 = 0,05 проверить гипотезу о том , что сгенерированные данные распределены по нормальному закону с заданными параметрами.
Варианты работы.
| № | ||||||||||
| N | ||||||||||
| s |
| № | ||||||||||
| N | ||||||||||
| s |
Методика выполнения работы
Пусть остатки от прогнозов подчиняются нормальному распределению с нулевым математическим ожиданием и средним квадратическим отклонением s. Генерация массивов в системе MATHCAD производится с помощью оператора Y:=rnorm(N,m,s). Данные, полученные в процессе генерации, упорядочены по возрастанию и разбиты на классы(разряды).
Результаты сведены в таблицу:
| Разряды | (-4)¸(-3) | (-3)¸(-2) | (-2)¸(-1) | (-1)¸ 0 | 0 ¸ 1 | 1 ¸ 2 | 2 ¸ 3 | 3 ¸ 4 |
| Частоты Рi* | 0,012 | 0,05 | 0,144 | 0,266 | 0,240 | 0,176 | 0,092 | 0,02 |
| Число попаданий в I –ый разряд |
Пользуясь критерием согласия c2 определить, не противоречит ли опытным данным гипотеза о том, что случайная величина Х распределена по нормальному закону с теми же параметрами ( mx = 0.168 ; sx = 1.448) .
Составим таблицу вероятностей попадания случайной величины Х, подчиненной нормальному закону ( 0,168 ; 1,448 ) в каждый из разрядов.
| Разряды | (-4)¸(-3) | (-3)¸(-2) | (-2)¸(-1) | (-1)¸ 0 | 0 ¸ 1 | 1 ¸ 2 | 2 ¸ 3 | 3 ¸ 4 |
| Частоты Рi | 0,0126 | 0,0522 | 0,1422 | 0,2433 | 0,2668 | 0,1789 | 0,0770 | 0,0212 |
| Частоты Рi* | 0,012 | 0,05 | 0,144 | 0,266 | 0,240 | 0,176 | 0,092 | 0,02 |
| Число попаданий в I –ый разряд |
Вероятности Рiвычисляем следующим образом:
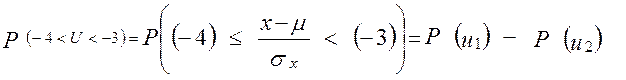
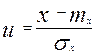
Вычисляем: 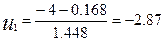
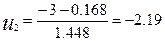
Так как нормальное распределение симметрично, то
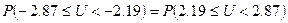 .
.
Находим по таблицам нормального распределения
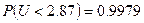
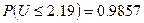
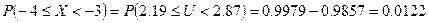
( В таблице Рi = 0,0126 . Расхождение связано с погрешностями округления. )
Таким образом, npi = 500*0,0126 = 6,3.
Аналогичным образом проводим вычисления для всех разрядов.
Так как по выборке оценивалось 2 параметра : 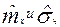 , то r = 8 – 1– 2 = 5
, то r = 8 – 1– 2 = 5
Вычисляем статистику 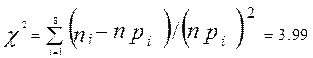
Критическое значение 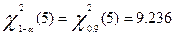
Lt; 9.236
Гипотеза о нормальности принимается !
Дата добавления: 2016-02-09; просмотров: 1074;
