Тема 2.2 Анализ точности вычислительных алгоритмов (алгоритмов оценивания состояния систем с неполной матрицей наблюдений)
2.2.1Одним из основных показателей качества вычислительных алгоритмов является их точность. В алгоритмах оценивания состояния точность определяется ошибкой (погрешностью) оценок. В системах с неполной матрицей наблюдений, когда шумами измерений можно пренебречь, эта погрешность равна для всех составляющих вектора состояния м определяется погрешностью оценки состояния опорного элемента.
В частности, для эталонов времени и частоты оценки относительных отклонений частоты 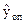 опорного элемента (хранителя частоты) при субоптимальной фильтрации, т.е. при использовании прогнозирующих моделей находится из соотношения
опорного элемента (хранителя частоты) при субоптимальной фильтрации, т.е. при использовании прогнозирующих моделей находится из соотношения
 , (65)
, (65)
где 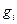 - вес i-го элемента группового эталона,
- вес i-го элемента группового эталона,
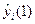 - прогноз i-ой составляющей вектора Y, вычисленный с упреждением на один шаг.
- прогноз i-ой составляющей вектора Y, вычисленный с упреждением на один шаг.
В выражении (65) опущен индекс t, поскольку подразумевается, что эти оценки справедливы для каждого такта обработки данных. Веса gi выбираются обратно пропорционально дисперсии прогнозов, причём веса нормированы таким образом, что их сумма равна единице. Погрешность такого алгоритма равна разности «истинного» значения уоп и его оценки, вычисленной по формуле (65), т.е.
е1=у- 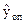 =
=  (66)
(66)
Для алгоритма, использующего оценки МНК, соответствующая погрешность равна
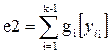 (67)
(67)
Из выражения (66) следует, что точность алгоритма, использующего прогнозирующие модели, стремится к нулю при возрастании точности прогнозов, что дает возможность повышения качества алгоритма за счет применения более точных моделей исследуемых процессов.
Алгоритм, использующий МНК-оценки, таким свойством не располагает.
2.2.2Теоретическая оценка точности алгоритмов обработки результатов измерений в недоопределенных линейных системах находится с помощью выражений (66), (67). Однако, в каждом конкретном случае качество алгоритма зависит от точности прогнозов. Исследовать качество прогнозов в общем случае целесообразно методами статистического моделирования.
Рассмотрим подобный подход к моделированию алгоритмов обраьотки данных в эталонах времени и частоты
Прогнозирующие модели строятся на методике Бокса-Дженкинса при наличии исходных временных рядов, которые можно рассматривать в качестве обучающей выборки.
Проблемы построения таких моделей для приборов, входящих в состав эталонов времени и частоты, заключаются в отсутствии данных об относительных отклонениях частоты для каждого из элементов группового эталона. Имеются лишь результаты косвенных измерений – относительные разности частот опорного и i-го стандарта, 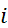 =1, 2,…,
=1, 2,…,  , где
, где  –число стандартов в эталоне. Как уже упоминалось выше, мы имеем дело с недоопределенной системой. Оценка состояния опорного элемента
–число стандартов в эталоне. Как уже упоминалось выше, мы имеем дело с недоопределенной системой. Оценка состояния опорного элемента 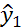 – относительное отклонение его частоты от «истинного значения» в момент времени
– относительное отклонение его частоты от «истинного значения» в момент времени 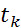 ,
,  может быть найдена при статистической обработке данных путем минимизации функционала
может быть найдена при статистической обработке данных путем минимизации функционала
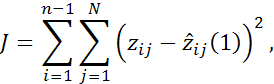
где 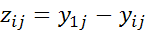 –результат i-го измерения, выполненного в момент
–результат i-го измерения, выполненного в момент 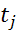 ,
,  - прогноз этого измерения. Т.к. прогнозы
- прогноз этого измерения. Т.к. прогнозы 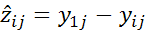 зависят от параметров прогнозирующих моделей:
зависят от параметров прогнозирующих моделей: 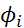 –коэффициенты авторегрессии и
–коэффициенты авторегрессии и 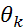 –коэффициенты скользящего среднего (
–коэффициенты скользящего среднего ( 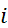 =1, 2,…,
=1, 2,…, 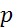 ,
, 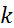 =1, 2,…,
=1, 2,…, 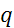 ), то задача минимизации функционала
), то задача минимизации функционала  сводится к поиску векторов параметров моделей
сводится к поиску векторов параметров моделей 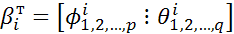 для всех стандартов, входящих в состав эталона.
для всех стандартов, входящих в состав эталона.
В работе [2] продемонстрировано применение данного подхода к задаче оценивания состояния вторичного эталона времени и частоты ВЭТ 1-5 ВСФ ВНИИФТРИ. По результатам взаимных измерений. Показано, что сумма квадратов отклонения оценок относительных отклонений частоты опорного стандарта от значений, найденных с помощью системы ГЛОНАС, снижается примерно на 9%, по сравнению с оценками метода наименьших квадратов (МНК-оценки). Кажущееся незначительным повышение эффективности алгоритма оценивания, основанного на использовании прогнозов вектора состояния эталона, на самом деле связано с серьезным экономическим эффектом, поскольку прирост точности эталона за счет привлечения новых, более точных, технических средств требует больших капиталовложений.
Однако, оценка эффективности алгоритмов обработки данных, получаемых в процессе функционирования эталонов времени и частоты, на основе их сличения с Государственным эталоном не является единственным из возможных методов. Более того, оценки состояния Государственного эталона сами содержат погрешности (как и вообще все оценки). Кроме того, погрешности канала сличения (система ГЛОНАС) также вносят дополнительный вклад в погрешность оценивания вектора состояния вторичного эталона.
Поэтому представляется весьма важным использовать подход к оцениванию точности алгоритмов обработки данных, получаемых в групповых эталонах, на основе методов статистического моделирования.
Особого внимания заслуживают следующие моменты:
- Генерация (имитация) временных рядов Y(t), обладающих заданными статистическими свойствами.
- Имитация рядов наблюдений  и оценка параметров моделей в недоопределенных системах на основе минимизации критерия
и оценка параметров моделей в недоопределенных системах на основе минимизации критерия 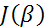 .
.
- Исследование рядов остатков 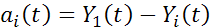 и проверка адекватности построенных моделей.
и проверка адекватности построенных моделей.
Введем ряд ограничений, вытекающих из изложенного выше подхода к поставленной задаче моделирования (мы не предполагаем всестороннего изучения процессов идентификации недоопределенных систем, а рассматриваем лишь отдельные, ключевые, моменты в этой процедуре).
1. Исходя из потребностей исследуемых вреальных систем (вторичные эталоны времени и частоты) будем считать ряды измерений, а, следовательно, и ряды исходных данных, равнопромежуточными, т.е. будем считать, что мы работаем с данными, полученными на суточных интервалах.
2. Шумами измерений при обработке данных на суточных интервалах можно пренебречь.
3. Поскольку наша задача - выявление основных закономерностей, проявляющихся при идентификации недоопределенных систем, то не имеет смысла рассмотрение всего множества моделей авторегрессии – скользящего среднего. Ограничимся лишь самыми простыми моделями – моделями авторегрессии (АР) первого порядка.
4. Будем считать достаточным рассмотрение моделей класса АР, т.е. откажемся от использования разностных рядов, а, следовательно, и термина «проинтегрированные» применительно к динамическим стохастическим моделям.
Исходя из поставленных задач и вытекающих из них ограничений, рассмотрим инструментальные средства, которые целесообразно использовать при моделировании процессов построения моделей авторегрессии скользящего среднего (АРСС). Прежде всего, отметим, что разработка специализированных систем моделирования в настоящее время может рассматриваться как определенное «архитектурное излишество», требующее значительных затрат времени исследователя, поскольку поставленную задачу можно решить, использую программные средства компьютерной математики: MATLAB, MATHCAD, STATISTICA, и т.д. Наиболее универсальной системой из перечисленных выше, безусловно, является MATLAB. Однако, несмотря на множество существующих ограничений, для решения многих проблем можно использовать систему MATHCAD. Более того, MATHCADможет быть с успехом применен и в более сложных задачах, таких как задачи субоптимальной фильтрации, рекуррентного оценивания состояний и т.д. Учитывая значительно меньшую стоимость этой системы, а также простую процедуру обмена данными с другими системами (в частности с ППП «STATISTICA») целесообразно использовать для наших целейименно MATHCAD. Это решение позволило объединить процесс изучения процедуры идентификации недоопределенных систем с процессом модернизации алгоритмов построения прогнозирующих моделей, т.е., по существу, решить проблему работы с ППП «MATHCAD» и «STATISTICA» в интерактивном режиме.
Рассмотрим процедуру генерации процессов авторегрессии с использованием MATHCAD при следующих значениях параметров временного ряда:
σ2 – дисперсия белого гауссова шума – 0,01 (СКО σ = 0,1)
YY1 – начальное значение ряда – 0
n– длина временного ряда = 200
ᵩ1– коэффициент авторегрессии = 0,8
Фрагмент ряда 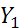 (первые 20 точек) приведен на рис. 1.
(первые 20 точек) приведен на рис. 1.

Рис.4 Фрагмент временного ряда, сгенерированного с помощью модели АР(1), φ1=0.8
Видно, что данный ряд, сформированный с помощью MATHCAD– программы (рис. 5), имеет сильную положительную корреляцию.

Рис. 5. Фрагмент программы генерации временных рядов
Рассмотрение частной автокорреляционной функции (рис. 6) подтверждает это предположение.
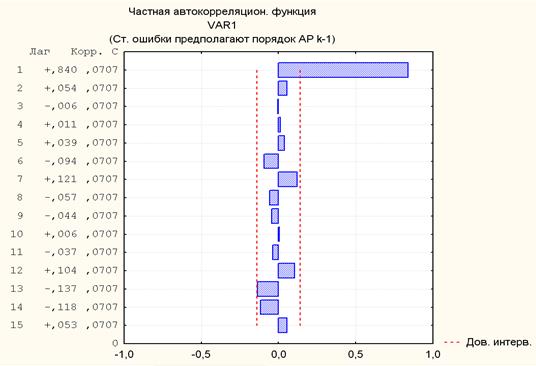
Рис. 6 Частная автокорреляционная функция
Модель АР, построенная для сгенерированного ряда с помощью ППП «STATISTICA», дает ту же самую оценку ( 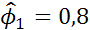 ).
).
Влияние дисперсии шума 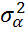 «возбуждающего систему» оценивалось генерацией процессов АР(1) – авторегрессии 1-го порядка. При разном уровне шума
«возбуждающего систему» оценивалось генерацией процессов АР(1) – авторегрессии 1-го порядка. При разном уровне шума 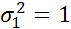 ,
,  , вид частной автокорреляционной функции не меняется. При достаточно большой выборке (
, вид частной автокорреляционной функции не меняется. При достаточно большой выборке ( 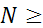 100), оценки параметров
100), оценки параметров 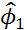 практически не зависят от уровня шума. Фрагменты временных рядов, полученных при указанных выше значениях
практически не зависят от уровня шума. Фрагменты временных рядов, полученных при указанных выше значениях 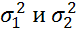 , приведены на рис. 7.
, приведены на рис. 7.
Таким образом, используя предложенную процедуру генерации временных рядов, мы можем получать временные ряды с заданными статистическими свойствами. Ряды наблюдений  получаются простым вычитанием членов выборки, соответствующих –му элементу группового эталона из «элементов» опорного стандарта частоты, т.е.
получаются простым вычитанием членов выборки, соответствующих –му элементу группового эталона из «элементов» опорного стандарта частоты, т.е. 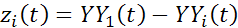 .
.
Полученный временной ряд можно рассматривать как недоопределенную систему (одно уравнение с двумя неизвестными: Y1 и Y2) и использовать для оценки состояния опорного элемент формулу (65).
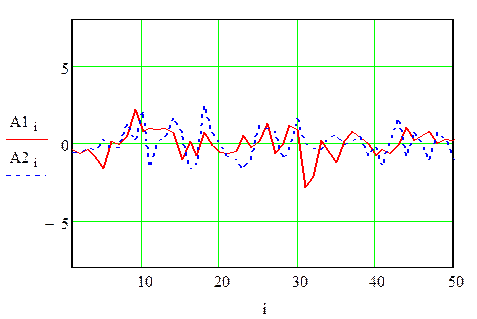
Рис. 7 Временные ряды, полученные при разных уровнях шумов
Следующим шагом является проверка адекватности построенных моделей. Ограничимся при этом только проверкой адекватности модели опорного элемента (точнее, модели временного ряда, построенной для относительных отклонений частоты опорного генератора эталона времени и частоты). Практически все критерии адекватности моделей АРСС основываются на анализе остаточных членов 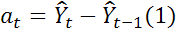 , вычисляемых как разность текущей оценки члена ряда
, вычисляемых как разность текущей оценки члена ряда 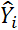 и ее прогноза
и ее прогноза 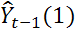 , вычисляемого на предыдущем шаге. Для адекватных моделей остаточные члены должны подчиняться нормальному закону и быть не коррелированными.[На рис. 8 приведена гистограмма ряда остатков, из которой видно, что распределение близко к нормальному.
, вычисляемого на предыдущем шаге. Для адекватных моделей остаточные члены должны подчиняться нормальному закону и быть не коррелированными.[На рис. 8 приведена гистограмма ряда остатков, из которой видно, что распределение близко к нормальному.
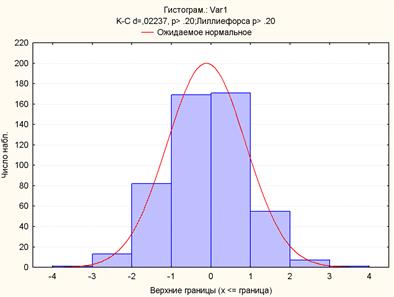
Рис. 8 Гистограмма ряда остатков
Более формальные методы основываются на использовании критерия Пирсона. Например, для ряда остатков, содержащего 100 точек, с математическим ожиданием 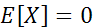 и единичной дисперсией (
и единичной дисперсией ( 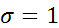 ) при разбиении на 16 разрядов (число степеней свободы
) при разбиении на 16 разрядов (число степеней свободы  ) получено значение
) получено значение 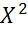 -статистики, равное 2,99, что соответствует вероятности
-статистики, равное 2,99, что соответствует вероятности 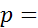 0,886 (Критическое значение
0,886 (Критическое значение  при уровне значимости 0,05 равно 23,68).Естественно, что при таких результатах гипотеза о нормальности остатков отброшена быть не может.
при уровне значимости 0,05 равно 23,68).Естественно, что при таких результатах гипотеза о нормальности остатков отброшена быть не может.
Наиболее общий подход к анализу адекватности моделей АРСС основывается на использовании совокупного критерия согласия [4], в котором анализируются значения корреляционной функции ряда остатков. Автокорреляционная функция вычислялась с помощью ППП «STATISTICA». Импорт ряда остатков, вычисляемых в MATHCADе, производится с помощью группы операторов
file:=”путь”, например,
file:=”D:\2\test.txt”
A:= ”идентификатор импортируемого файла”
writePRN(file):=A
После чего файл с именем ”file” вводится в ППП «STATISTICA» через буфер обмена. Автокорреляционные функции(ACR), вычисленные в ППП, представлены в таблице (K – номер лага)
| K | ||||||||||
| ACR | 0,004 | -0 | 0,024 | 0,002 | 0,030 | -0,038 | 0,019 | -0,081 | -0,034 | 0,088 |
| `4 | ||||
| 0,019 | 0,059 | -0,040 | 0,052 | 0,013 |
Совокупный критерий согласия вычисляется как

( 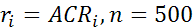 – объем выборки).
– объем выборки). 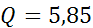 . Число степеней свободы
. Число степеней свободы 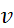 равно 14 (
равно 14 ( 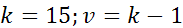 ).
).  - критическое значение величины
- критическое значение величины 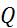 , подчиняется
, подчиняется 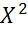 -распределению.На уровне значимости 0,05 равно 23,58. Вычисленное значение критерия 5,85<<23,58. Гипотеза об адекватности модели не отбрасывается и на основании совокупного критерия. Впрочем, подобный результат можно было предполагать и на основе простого рассмотрения ряда остатков.
-распределению.На уровне значимости 0,05 равно 23,58. Вычисленное значение критерия 5,85<<23,58. Гипотеза об адекватности модели не отбрасывается и на основании совокупного критерия. Впрочем, подобный результат можно было предполагать и на основе простого рассмотрения ряда остатков.
Таком образом, модели АР, построенные на основе минимизации функционала J, удовлетворяет требованиям адекватности, и могут быть использованы для вычисления краткосрочных прогнозов.
Дата добавления: 2016-02-09; просмотров: 1053;
