Условия стационарности и обратимости линейного процесса
Под стационарностью понимается неизменность статистических характеристик процесса во времени.
Условие стационарности рядов обеспечивается конечным значением дисперсии процесса. При этом автоковариации и автокорреляции должны удовлетворять ряду условий. Для линейного процесса эти условия могут быть объединены в одно, а именно, что ряд 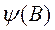 – производящая функция для весов
– производящая функция для весов 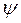 – должен сходиться при
– должен сходиться при  , т.е. для B, лежащих внутри или на единичной окружности.
, т.е. для B, лежащих внутри или на единичной окружности.
Для коэффициентов авторегрессии условие стационарности трансформируется в следующее требование 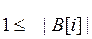 ,
, 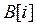 корни характеристического уравнения
корни характеристического уравнения 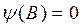 . То есть корни уравнения
. То есть корни уравнения 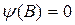 лежат вне или на единичном круге.
лежат вне или на единичном круге.
Исходя из условия стационарности, можно получить граничные условия для коэффициентов авторегрессии. Так как некоторые корни характеристического уравнения с обобщенными коэффициентами авторегрессии лежат на границе устойчивости, то есть, равны единице, то замена коэффициентов авторегрессии на коэффициенты обобщенной авторегрессии приводит к увеличению порядка используемой модели АРПСС.
Так для первого порядка авторегрессии границы стационарности
 (41)
(41)
Для уравнения второго порядка:
 (42)
(42)

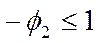
Для третьего порядка:
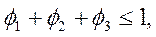 (43)
(43)

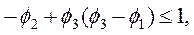
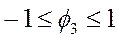
Выше было показано, что веса 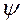 линейного процесса, если он стационарен, должны удовлетворять условию сходимости. Рассмотрим теперь ограничения, связанные с обратимостью процесса АРПСС. Условие обратимости предполагает возможность прогнозирования назад временного ряда. Оно не зависит от условий стационарности и применимо также к нестационарным линейным моделям. При прогнозировании назад значения временного ряда берут с весами
линейного процесса, если он стационарен, должны удовлетворять условию сходимости. Рассмотрим теперь ограничения, связанные с обратимостью процесса АРПСС. Условие обратимости предполагает возможность прогнозирования назад временного ряда. Оно не зависит от условий стационарности и применимо также к нестационарным линейным моделям. При прогнозировании назад значения временного ряда берут с весами 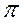 .
.
Если веса 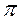 образуют сходящийся ряд, то такой ряд называется обратимым. Это условие будет выполняться, если корни уравнения
образуют сходящийся ряд, то такой ряд называется обратимым. Это условие будет выполняться, если корни уравнения  находятся внутри или на единичной окружности, то есть
находятся внутри или на единичной окружности, то есть 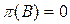 , при
, при 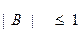 .
.
Таким образом, при переходе к оператору скользящего среднего (СС) налагается следующее ограничение на веса СС: корни уравнения оператора скользящего среднего  должны быть вне или на единичной окружности (
должны быть вне или на единичной окружности (  ).
).
Сходящиеся ряды возможны и в случае, когда  . При этом
. При этом 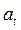 выражается только через
выражается только через 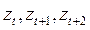 , то есть через настоящее и будущее значение процесса. Таким образом, требование обратимости необходимо, если мы заинтересованы в разумной связи текущих событий с событиями в прошлом.
, то есть через настоящее и будущее значение процесса. Таким образом, требование обратимости необходимо, если мы заинтересованы в разумной связи текущих событий с событиями в прошлом.
Подводя итоги, отметим, что линейный процесс стационарен, если 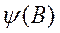 сходится внутри или на единичной окружности, и обратим, если
сходится внутри или на единичной окружности, и обратим, если  сходится той же области, и если
сходится той же области, и если 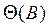 сходится вне или на единичной окружности, и обратим, если
сходится вне или на единичной окружности, и обратим, если 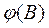 сходится в той же области.
сходится в той же области.
Так как условие обратимости аналогично условию стационарности, то границы обратимости будут совпадать с границами стационарности.
Границы обратимости для первого порядка:
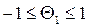 (44)
(44)
Границы обратимости для второго порядка:
 (45)
(45)
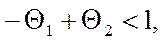
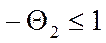
Границы обратимости для третьего порядка:
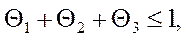 (46)
(46)
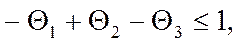

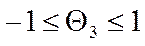
Дата добавления: 2016-02-09; просмотров: 1729;
