Прогнозирование процессов АРПСС
Использование доступных к моменту времени t наблюдений временного ряда для прогнозирования его значения в некоторый момент времени в будущем t + l может явиться основой для:
· планирования в экономике и торговле;
· планирования и выпуска продукции;
· складского контроля и контроля выпуска;
· управления и оптимизации промышленных процессов.
Следовательно, существует необходимость в прогнозе вперед на интервал, называемый временем упреждения и зависящий от конкретной проблемы. Например, время упреждения в задачах складского учета определено как период, начинающийся с момента передачи заказа на пополнение склада с завода и длящийся до тех пор, пока заказ не доставлен на склад.
Предполагается, что наблюдения доступны в дискретные равно отстоящие моменты времени. В задачах оценивания состояния опорного элемента в групповых эталонах (например, эталонах времени и частоты) наряду с результатами измерений, полученными на 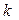 -ом такте, целесообразно использовать прогнозы относительных отклонений частоты водородных генераторов, вычисленные на один шаг вперед (выражение 2.3). Обозначим через
-ом такте, целесообразно использовать прогнозы относительных отклонений частоты водородных генераторов, вычисленные на один шаг вперед (выражение 2.3). Обозначим через 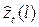 сделанный в момент t прогноз
сделанный в момент t прогноз 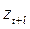 в некоторый момент t + l в будущем, т.е. с упреждением l.
в некоторый момент t + l в будущем, т.е. с упреждением l.
Функция 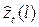 , l = 1,2,…, дающая в момент t прогнозы для всех будущих времен упреждения называется прогнозирующей функцией. При этом ставится задача получить такую прогнозирующую функцию, у которой среднее значение квадрата отклонения
, l = 1,2,…, дающая в момент t прогнозы для всех будущих времен упреждения называется прогнозирующей функцией. При этом ставится задача получить такую прогнозирующую функцию, у которой среднее значение квадрата отклонения 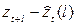 является наименьшим для каждого упреждения l. В дополнение к вычислению наилучшего прогноза необходимо также указать его точность, чтобы, например, можно было оценить риск, связанный с решениями, основанными на прогнозировании. Точность прогноза может быть выражена вероятностными пределами по обе стороны от каждого прогнозируемого значения. Эти пределы можно вычислять для любого удобного набора вероятностей, например, для 50 и 95%. Смысл этих пределов в том, что значение временного ряда, которое появится в соответствующее время, с указанной вероятностью будет лежать внутри этих пределов.
является наименьшим для каждого упреждения l. В дополнение к вычислению наилучшего прогноза необходимо также указать его точность, чтобы, например, можно было оценить риск, связанный с решениями, основанными на прогнозировании. Точность прогноза может быть выражена вероятностными пределами по обе стороны от каждого прогнозируемого значения. Эти пределы можно вычислять для любого удобного набора вероятностей, например, для 50 и 95%. Смысл этих пределов в том, что значение временного ряда, которое появится в соответствующее время, с указанной вероятностью будет лежать внутри этих пределов.
Прогноз с минимальной среднеквадратичной ошибкой 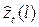 для упреждения l – это условное математическое ожидание
для упреждения l – это условное математическое ожидание 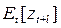 случайной величины
случайной величины 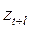 в момент времени t. Можно записать выражения для прогноза любым из трех различных способов, соответствующих трем способам представления модели, приведенным выше.
в момент времени t. Можно записать выражения для прогноза любым из трех различных способов, соответствующих трем способам представления модели, приведенным выше.
Если мы имеем значение ряда, то по формуле 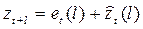 можно найти ошибку прогноза
можно найти ошибку прогноза 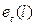 с упреждением l.
с упреждением l.
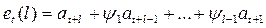 (56)
(56)
Математическое ожидание ошибки прогноза с упреждением и дисперсия ошибки прогноза V(l) равны
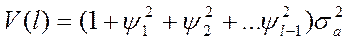 (57)
(57)
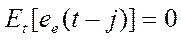
Условное математическое ожидание можно представить как

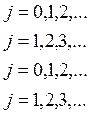 (58)
(58)
Существуют три основных представления прогноза, опирающиеся на разные формы описания моделей:
· прогнозы, полученные из разностного уравнения
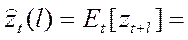 (59)
(59)

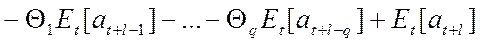
· прогноз в проинтегрированном виде
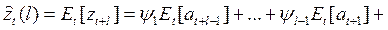 (60)
(60)

· прогноз как взвешенное среднее предшествующих наблюдений и прогнозов, сделанных в тот же момент с меньшими упреждениями
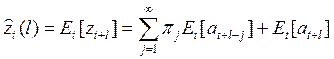 (61)
(61)
В двух последних случаях теоретически необходимо для предсказания величины знание всех прошлых z, либо а, до бесконечности. На практике, так как из условия стационарности и обратимости веса прямой и обращенной модели должны убывать, можно ограничиться некоторым конечным числом предшествующих членов ряда без потери точности прогнозирования.
Наиболее пригодной формой вычисления прогноза является форма, при которой используется разностное уравнение модели АРПСС. В общем случае дисперсия ошибки прогноза на l шагов вперед для любого момента t, определяемая как математическое ожидание величины  , равна
, равна
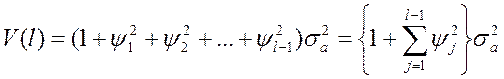 (62)
(62)
Из предположения, что а подчиняется нормальному закону, следует, что при известных значениях процесса до момента t условное распределение вероятности  будущего значения процесса
будущего значения процесса  будет также нормальным со средним значением
будет также нормальным со средним значением 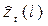 и стандартным отклонением
и стандартным отклонением
 (63)
(63)
Вероятностные пределы будут иметь вид
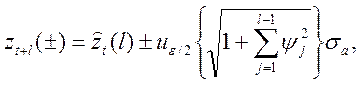 (64)
(64)
где 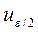 – это квантиль уровня
– это квантиль уровня 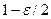 стандартного нормального
стандартного нормального
распределения.
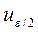 равно 0.68; 1.65; 1.96 или 2.58 в зависимости от того, лежит ли
равно 0.68; 1.65; 1.96 или 2.58 в зависимости от того, лежит ли
будущее значение между пределами с вероятностью 50; 90; 95 или 99 процентов соответственно.
2.1.7 Идентификация структуры моделей
Бокс и Дженкинс [1] разделяют задачу построения моделей АРПСС на два этапа. Вначале решается задача идентификации структуры модели, т.е. определения p и q. Для этого применяется понятие “близости” или “похожести” теоретических автокорреляционных функций процессов АРПСС их оценкам, найденным по эмпирическим временным рядам. Затем ищутся оценки параметров моделей методом их “подгонки”.
Автокорреляционные функции (ACR) определяют «статистическую близость» членов временного ряда как функцию временной задержки (лагов). Частная автокорреляционная функция (PACR) рассчитывается на основе ACR и характеризует близость членов временного ряда при исключенном влиянии промежуточных членов. Оценки ACR и PACR как функции
«лагов » можно вычислить с помощью ППП STATISTICA. В рассмотренном ниже примере приведены графики этих функций для некоторого временного ряда и кратко описана процедура идентификации структуры модели АРСС ( в аббревиатуре отсутствует буква «П», так как анализируемый временной ряд не содержит трендов ( ни детерминированных, ни стохастических) и, стало быть может быть описан простыми моделями авторегрессии – скользящего среднего).
Приведём полученные автокоррелограммы и частные автокоррелограммы для полученных рядов оценок среднего (рис. 3).
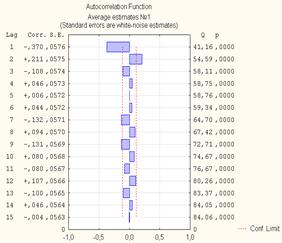
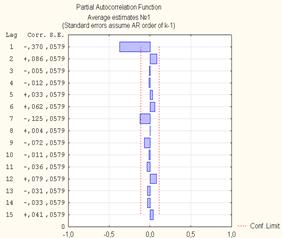
Рис.3 – Выборочные АКФ и ЧАКФ оценок ряда
Проанализируем полученные автокоррелограммы. Как известно, структура модели АРПСС кратко записывается как (p,d,q), где p – порядок процесса АР, q – порядок процесса СС, а d – порядок разности процесса (в нашем случае всегда равен 0).
Для ряда можно предположить как модель структуры (1,0,0), так и модель (0,0,1), наиболее предпочтительным выглядит первый вариант.
После того, как определена структура модели, выбором соответствующего режима пакета STATISTICA производится подгонка параметров модели, т.е. находятся оценки параметров АР и СС.
Дата добавления: 2016-02-09; просмотров: 1042;
