Оценивание состояния недоопределенных динамических систем
( групповые эталоны)(Интерактивное обучение -150 минут)
Цель работы: освоение методов конструирования вычислительных алгоритмов для оценивания состояния систем с неполной матрицей наблюдений
Групповые эталоны создаются для повышения точности и надежности хранения единиц физических величин. Примером такого эталона является эталон времени и частоты. В процессе функционирования эталонов проводятся регулярные измерения (сличения) единиц физических величин, воспроизводимых каждым из элементов, входящих в состав эталона.
При этом реализована схема “опорный с каждым”, при которой один из элементов) выбирается в качестве опорного (пусть, для определенности, это будет первый элемент ). В определенный момент времени производятся измерения разностей :
zi = yоп – уi, где
уi - значение величины, воспроизводимой i-тым элементом, (i=  ), n- число элементов группового эталона.
), n- число элементов группового эталона.
Таким образом, в момент времени t получается n-1 результатов измерения:
z1 = y1 – у2 ; z2 = y1 – у3 ;…; zn-1 = y1 – уn
Обозначив набор значений уi (i=  ), как вектор У, а набор результатов измерений zy , как вектор Z, получим матричное уравнение
), как вектор У, а набор результатов измерений zy , как вектор Z, получим матричное уравнение
Z(t)=H*Y(t) (1)
Матрица измерений Н для данной схемы имеет вид:
Н= 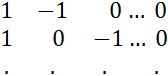
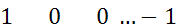
Размерность матрицы (n-1)*n
Решение системы, имеющее минимальную норму имеет общий вид
Y=H+ *Z, (2)
где H+ - псевдообратная матрица.
В дальнейшем, индекс t при записи уравнений, опускается.
Нам, в принципе, достаточно найти оценку значения опорного элемента –  , поскольку оценки всех остальных элементов найдутся из результатов измерений
, поскольку оценки всех остальных элементов найдутся из результатов измерений
zi = y1 – уi , при подстановке вместо значения у1, его оценки  .
.
При данной схеме “сличений” , а стало быть и матрице измерений Н, оценка значения состояния у, найдется как среднее арифметическое результатов измерений
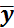 1=
1= 
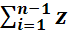 i(3)
i(3)
Формула справедлива для каждого момента времени t.
Найденная оценка  и оценки всех остальных состояний называются оценками метода наименьших квадратов (МНК-оценками).
и оценки всех остальных состояний называются оценками метода наименьших квадратов (МНК-оценками).
Оценками состояния недоопределенных систем можно улучшить, если для их вычисления использовать не только результаты измерений zi, выполненные в данный момент времени, но и прогнозы вектора состояния
Уt-1(1), вычисленные на предыдущем такте обработки данных. Тогда оценка состояния опорного элемента найдется как
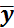 1(t) =
1(t) =  i(1)(4)
i(1)(4)
В формулу (1) добавлено одно фиктивное измерение z1 = y1 – у1 =0
Очевидно, что оценка (4), которая соответствует алгоритму фильтрации, будет более точной, чем оценка (3).
Задание на работу:
1. Сформулируйте “ряды вычислений”, вычитая из ряда y1(t), ряды y2(t) и y3(t), построенные в работе 1.
2. Используя модели AP, полученные в работе 2, найдите оценку состояния опорного элемента по формулам (3) и (4). В формуле (4) прогноз вычисляется как 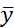 i(1) =
i(1) = 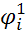 *
* 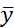 i(t-1)
i(t-1)
3. Найдите сумму квадратов отклонений оценок 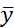 1 , от их истинных значений, то есть значений ряда у1, сгенерированных в лабораторной работе 1.
1 , от их истинных значений, то есть значений ряда у1, сгенерированных в лабораторной работе 1.
 i)2
i)2
N=100
Оценки 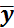 1 , соответствующей формулам (3) и (4).
1 , соответствующей формулам (3) и (4).
4. Постройте графики y1(t) , y2(t), y3(t), 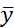 1(t),
1(t), 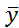 2(t),
2(t), 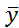 3(t).
3(t).
5. Найдите среднее значение отклонений
yi(t) - 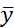 i(t)
i(t)  i=1,2,3
i=1,2,3
и оценку дисперсии этих отклонений
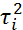 =
= 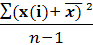
Пример MATHCAD – программы для двух временных рядов приведен ниже. Обобщение данной программы для n=3 очевидно и не требует дополнительных объяснений.
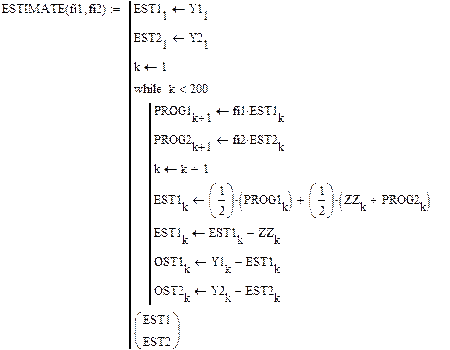
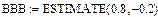
Дата добавления: 2016-02-09; просмотров: 944;
