Модели авторегрессии и скользящего среднего

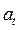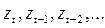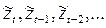Модель авторегрессии является исключительно полезной стохастической моделью для описания некоторых встречающихся на практике рядов. В этой модели текущее значение процесса выражается как конечная линейная сово­купность предыдущих значений процесса и импульса . Обозначим значения процесса в равноотстоящие моменты времени t, t-1, t-2,… как Пусть будут отклонениями от среднего значения 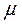, например 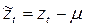. Тогда

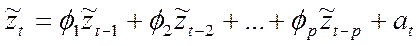(33)

называется процессом авторегрессии (АР) порядка .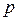

В (3.5) переменная 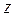регрессирует на своих предшествующих значениях; поэтому модель авторегрессирующая. Если мы определим оператор авторегрессии порядка 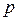как

(34)
то модель авторегрессии можно сжато описать как

(35)

Модель авторегрессии (3.5) выражает отклонение 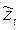, процесса в виде конечной взвешенной суммы 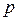предыдущих отклонений процесса
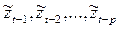плюс случайный импульс 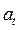или выражает как бесконечную взвешенную сумму .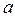

Если линейно зависит от конечного числа 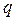предыдущих 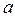– такой процесс называется процессом скользящего среднего (СС) порядка :

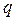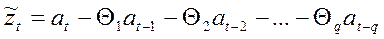(36)

Если определить оператор скользящего среднего порядка 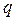как

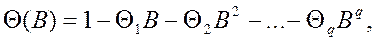(37)

то модель скользящего среднего можно сжато записать как

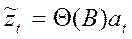(38)

Для достижения большей гибкости в подгонке моделей к наблюдаемым
временным рядам иногда целесообразно объединить в одной модели и авторегрессию, и скользящее среднее. Это приводит к комбинированной модели авторегрессии – скользящего среднего

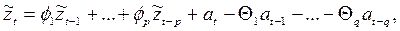(39)

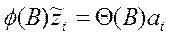или (40)

На практике часто оказывается, что адекватное описание наблюдаемых
временных рядов достигается при помощи моделей авторегрессии, скользящего среднего или комбинированной модели, в которых 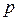и 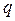не больше, а часто и меньше