Задача оценки состояния недоопределенных систем

Типичным случаем недоопределённых систем являются групповые эталоны. В частности, эталоны времени и частоты, в которых в качестве вектора состояния рассматриваются относительные отклонения частоты стандартов, входящих в состав эталона. Структурная схема измерений, выполненных в таких эталонах, приведена на рисунке 2.

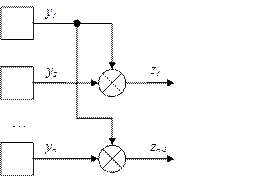
Рис. 2 – Структурная схема измерений

Если пренебречь шумами измерительной системы, а для измерений, выполняемых на суточных интервалах, это вполне допустимо, то для нахождения вектора состояния эталона достаточно получить оценку состояния опорного элемента (на рис. 2 это первый элемент). Оценки других составляющих вектора состояния найдутся немедленно из результатов измерений, выполненных на k-м такте.

В групповых эталонах измерения выполняются путем сличения их элементов друг с другом. Чаще всего применяется схема сличения всех элементов с одним из них, выбранным в качестве «опорного». Без потери общности будем считать опорным первый элемент. Тогда матрица измерений имеет вид

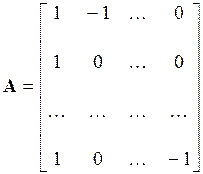(24)

Размерность матрицы - (n-1) *(n).

Эталоны времени и частоты можно рассматривать как динамические системы, в которых вектор состояния представлен в виде относительных отклонений частот квантово-механических генераторов, входящих в состав эталона. С течением времени относительные отклонения частот – y_i меняют свои значения. Результаты измерений, выполненных в момент времени t_j, –

z_ji= y_j1 – y_j,i+1 (25) ,

где j = 1,2, …

i = 1,2,…,n-1

В уравнении (25) предполагается, что измерения выполняются через равные интервалы времени.

Различаются два режима обработки данных: статический и динамический. В статическом режиме предполагается, что все данные, полученные с момента t=1 до t=N , имеются в распоряжении исследователя и могут обрабатываться одновременно. При обработке данных в динамическом режиме используются результаты измерений, выполненных в момент t_k, и априорная информация об объекте, чаще всего представленная в виде прогнозов вектора состояния. Как правило, прогнозы вычисляются на основе математической модели, описывающей динамику объекта. Оптимальные оценки вектора состояния в динамическом режиме обработки данных находятся с помощью рекуррентных соотношений, известных как фильтр Калмана . предложен алгоритм субоптимальной фильтрации для измерительных систем с матрицей измерений вида (24). Оценка состояния опорного элемента на момент t_j в этом алгоритме находится из соотношения

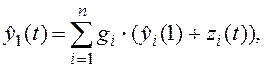(26)

где 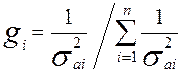- вес i-го прогноза ,

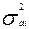- дисперсия прогноза i – ой составляющей вектора состояния,

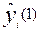- прогноз i – ой составляющей вектора Y, полученный на предыдущем такте обработки данных.

Вектор Zв выражении (9) дополнен фиктивной составляющей z₁ = y₁ – y₁ = 0 , поэтому размерности векторов Zи 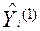совпадают.

Альтернативный алгоритм основан на использовании МНК – оценок, вычисленных с помощью псевдообратной матрицы.

Псевдообратная матрица в нашем случае вычисляется по формуле

А⁺ = А^T (AA^T) ^-1 и имеет вид

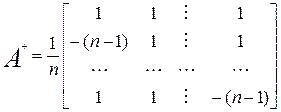
При этом оценка вектора состояния находится по формуле 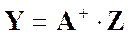(27)

(27)

Или, в развернутом виде,

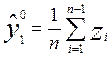
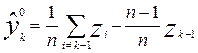, k = 2,3,…, n (28)

Очевидно, что МНК- оценка опорного элемента на k-м шаге совпадает со средним значениям результатов измерений.

Т.о. имеем два класса алгоритмов вычисления вектора состояния недоопределенных систем:

- алгоритм среднего арифметического – МНК – оценки;

- алгоритм, опирающийся на использовании прогнозирующих моделейю