Раздел 2. Прогнозирующие модели и их построение по эмпирическим данным

Тема 2.1 Модели авторегрессии – проинтегрированного скользящего среднего

Идея использования математических моделей для описания поведения физических объектов является общепризнанной. В частности, иногда удается по­учить модель, основанную на физических законах, что дает возможность вы­числить почти точное значение какой-либо зависящей от времени величины в любой момент времени. Например, мы можем вычислить траекторию ракеты, запущенной в известном направлении с известной скоростью. Если были бы известны точные значения всех исходных данных, такая модель была бы целиком детерминированной.

Однако в данной задаче могут иметь место ряд неизвестных факторов, на­пример переменная скорость ветра, которая может слегка отклонить ракету от курса. Во многих проблемах необходимо исследовать объекты, зависящие от времени, например, такие как месячный сбыт газетной бумаги, уровень воды в водоеме, стоимость курса акций и так далее. Для таких объектов нельзя пред­ложить детерминированную модель, допускающую точное вычисление буду­щего поведения объекта. Тем не менее, можно разработать модель, позволяю­щую вычислить вероятность того, что некоторое будущее значение будет ле­жать в определенном интервале. Такая модель называется вероятностной или стохастической. Модели временных рядов, необходимые для получения оптимального прогнозирования и регулирования, в действительности являются сто­хастическими. Также необходимо различать вероятностную модель (иначе стохастический процесс), и наблюдаемый временной ряд.

Важный класс стохастических моделей для описания временных рядов – это так называемые стационарные модели. Они основаны на предположении, что процесс остается в равновесии относительно постоянного среднего уровня. Однако, ограничиваясь только применением стационарных моделей в прогно­зировании, мы существенно сужаем круг решаемых задач.

Для снятия этого ограничения применяются нестационарные модели, не имеющие естественного среднего значения. Нестационарные процессы описы­ваются моделями авторегрессии — проинтегрированного скользящего среднего (АРПСС). Этот широкий класс моделей описывает множество как стационар­ных, так и нестационарных процессов (стационарно-разностных процессов).

Подход к прогнозированию заключается в выборе структуры стохастиче­ской модели для исследуемого временного ряда. По имеющейся выборке ис­ходных данных подгоняются параметры модели. Затем с ее помощью находится оптимальная прогнозирующая функция.

Основные операторы

Для описания моделей АРПСС используются следующие операторы:

· Оператор сдвига назад В определяется как

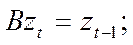(29)

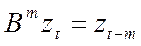
· Оператор сдвига вперед F

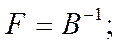(30)

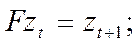
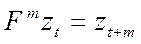
· Разностный оператор со сдвигом назад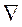

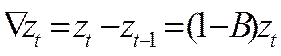(31)

· Оператор суммирования

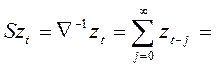(32)

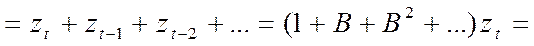
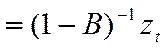
2.1.2 “Белый шум”

Временные ряды, в которых последовательные значения сильно зависимы, целесообразно рассматривать как генерируемые последовательностью незави­симых импульсов 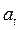. Эти импульсы – реализации случайных некоррелирован­ных величин с фиксированным распределением, которое обычно предполагает­ся нормальным с нулевым средним значением и дисперсией 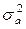. Такая после­довательность случайных величин 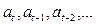называется в технической ли­тературе «белым шумом».