Задача оценки состояния реальной системы

Существует очень широкий класс прикладных задач, где требуется определять и прогнозировать состояния самых различных физических объектов, в том числе и в целях управления. Состояние объекта характеризуется совокупностью некоторых параметров, которые необходимо определить в результате обработки и анализа данных, полученных в процессе наблюдения за объектом. В общем случае это можно представить следующей схемой (рис.1) :

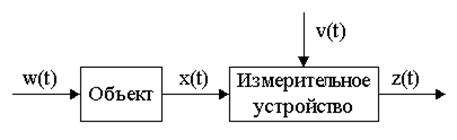
Рис.1 Задача оценки.

Здесь w(t) – вектор действующего на систему шума, x(t) – выходной сигнал системы, z(t) – измеренный выходной сигнал системы, v(t) – вектор шумов измерения.

При этом фактическое состояние любой реальной системы может быть полностью описано лишь бесконечным (или практически бесконечным) числом параметров. С другой стороны, в распоряжении исследователя, приступающего к решению рассматриваемой задачи, всегда имеется только конечное число независимых измерений, искаженных неизбежными ошибками. Поэтому полное определение состояния реальной системы по данным измерений практически невозможно. Речь может идти лишь о получении некоторой его оценки. При этом реальная система заменяется ее математической моделью, зависящей от конечного числа параметров. Так, например, при решении большинства задач небесной механики Солнечная система, представляющая собой совокупность гигантских тел, в которых непрерывно происходят сложнейшие физико-химические процессы, заменяется простой системой, состоящей из конечного числа материальных точек. Каждая из этих точек представляет соответствующее небесное тело, ее состояние полностью описывается семью величинами – массой и шестью элементами ее орбиты. Поэтому полное состояние такой упрощенной модели Солнечной системы описывается конечным числом параметров.

При решении различных прикладных задач одна и та же реальная система может представляться различными математическими моделями. Выбор используемой математической модели зависит от природы исследуемой системы и существа решаемой задачи. Однако во всех случаях состояние этой модели должно полностью определяться конечным числом параметров q₁, q₂, … , q_m, совокупность которых называется вектором состояния

q = {q₁, q₂, … , q_m}. (12)

Число m составляющих вектора q называется размерностью модели (или задачи).

Для определения вектора q используются измерения некоторых величин, зависящих от состояния системы. Совокупность всех используемых измерений образует вектор измерений:

d = {d₁, d₂, … , d_n}, (13)

где n – число измерений. Для того чтобы по измеренному значению вектора d оценить соответствующий вектор q, необходимо знать зависимость между ними. Для принятой математической модели она имеет вид

d = F(q). (14)

Однако в действительности измеренные значения составляющих вектора d получаются в результате наблюдений за состоянием реальной системы, в то время как зависимость (14) соответствует принятой математической модели. Обозначим через h = {h₁, h₂, … , h_n} вектор ошибок этой модели

h = d_И– F(q_И), (15)

где d_Ииq_И – истинные значения соответствующих векторов. Погрешности h иногда называют методическими ошибками.

Пусть 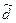– значение вектора d, полученное в результате измерений. Оно связано с d_и соотношением:

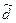= d_{И +} j , (16)

где j = {j₁, j₂, … , j_n} – вектор ошибок измерений. Из (15) и (18) следует, что

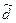= F(q_И) + j + h. (17)

При решении рассматриваемой задачи точные значения векторов jиh остаются неизвестными. Их обычно рассматривают как случайные векторы с заданными вероятностными характеристиками (законами распределения, моментами и т.п.). При этом зависимость (17) заменяется так называемой системой условных уравнений:

F(q) = 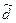, (18)

представляющей собой систему из n уравнений относительно m неизвестных q₁, q₂, … , q_m. Система условных уравнений является неточной и из нее нельзя получить истинное значение q_И вектора состояния. Может быть найдена лишь некоторая оценка 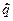этого вектора. Она должна по возможности мало отличаться от q_И. При этом задача сводится к отысканию алгоритма вида

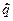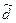= Ф( ), (19)

позволяющего находить оценку 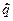по измеренному значению .

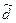Структура этого алгоритма зависит от вида системы условных уравнений (18) и имеющихся сведений об ошибках jиh. Основной задачей этого алгоритма является возможное уменьшение (фильтрация) влияния этих ошибок. Его обычно называют алгоритмом фильтрации.

Полученная в результате оценка 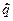, как правило, не удовлетворяет системе условных уравнений (18). После подстановки этой оценки в левую часть указанной системы получаем зависимость вида

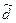= F( 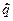) + d, (20)

где d = {d₁, d₂, … , d_n} – так называемый вектор невязок.

Из изложенного следует, что задача построения алгоритма фильтрации является неоднозначной. Поэтому возникает вопрос о выборе в некотором смысле оптимального алгоритма фильтрации. При этом нужно исходить из того, что любой используемый на практике алгоритм фильтрации должен обладать следующими свойствами:

· Определяемая зависимость (19) должна быть однозначной (для данного алгоритма).

· В предположении об отсутствии ошибок измерений и модели он должен давать истинное значение вектора состояния. Иначе говоря, должно удовлетворяться так называемое условие несмещенности алгоритма фильтрации:

q = Ф[F(q)]. (21)

Наряду с задачей нахождения оценки 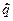возникает проблема оценки точности полученного результата, т.е. оценки погрешности

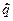( = – q_И. (22)

Последняя зависит от алгоритма (19), а также от ошибок jиh. Если при некоторых условиях, налагаемых на указанные ошибки, справедливы равенства

E(() = 0 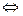E( 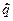) = q_И, (23)

то говорят, что при этих условиях оценка 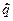является несмещенной.

В некоторых прикладных задачах вектор q может рассматриваться как случайная величина. В этих условиях представляет интерес либо задача оценки конкретной частной реализации этого вектора, либо определение его математического ожидания E(q).