Примеры хеш-функций
Выбираемая хеш-функция должна легко вычисляться и создавать как можно меньше коллизий, т.е. должна равномерно распределять ключи на имеющиеся индексы в таблице. Конечно, нельзя определить, будет ли некоторая конкретная хеш-функция распределять ключи правильно, если эти ключи заранее не известны. Однако, хотя до выбора хеш-функции редко известны сами ключи, некоторые свойства этих ключей, которые влияют на их распределение, обычно известны. Рассмотрим наиболее распространенные методы задания хеш-функции.
Метод деления. Исходными данными являются – некоторый целый ключ key и размер таблицы m. Результатом данной функции является остаток от деления этого ключа на размер таблицы. Общий вид функции:
int h(int key, int m) {
return key % m; // Значения
}
Для m = 10 хеш-функция возвращает младшую цифру ключа.
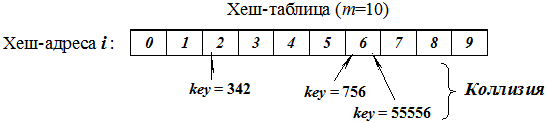
Для m = 100 хеш-функция возвращает две младшие цифры ключа.

Аддитивный метод, в котором ключом является символьная строка. В хеш-функции строка преобразуется в целое суммированием всех символов и возвращается остаток от деления на m (обычно размер таблицы m = 256).
int h(char *key, int m) {
int s = 0;
while(*key)
s += *key++;
return s % m;
}
Коллизии возникают в строках, состоящих из одинакового набора символов, например, abc и cab.
Данный метод можно несколько модифицировать, получая результат, суммируя только первый и последний символы строки-ключа.
int h(char *key, int m) {
int len = strlen(key), s = 0;
if(len < 2) // Если длина ключа равна 0 или 1,
s = key[0]; // возвратить key[0]
else
s = key[0] + key[len–1];
return s % m;
}
В этом случае коллизии будут возникать только в строках, например, abc и amc.
Метод середины квадрата, в котором ключ возводится в квадрат (умножается сам на себя) и в качестве индекса используются несколько средних цифр полученного значения.
Например, ключом является целое 32-битное число, а хеш-функция возвращает средние 10 бит его квадрата:
int h(int key) {
key *= key;
key >>= 11; // Отбрасываем 11 младших бит
return key % 1024; // Возвращаем 10 младших бит
}
Метод исключающего ИЛИ для ключей-строк (обычно размер таблицы m=256). Этот метод аналогичен аддитивному, но в нем различаются схожие слова. Метод заключается в том, что к элементам строки последовательно применяется операция «исключающее ИЛИ».
В мультипликативном методе дополнительно используется случайное действительное число r из интервала [0,1), тогда дробная часть произведения r*key будет находиться в интервале [0,1]. Если это произведение умножить на размер таблицы m, то целая часть полученного произведения даст значение в диапазоне от 0 до m–1.
int h(int key, int m) {
double r = key * rnd();
r = r – (int)r; // Выделили дробную часть
return r * m;
}
В общем случае при больших значениях m индексы, формируемые хеш-функцией, имеют большой разброс. Более того, математическая теория утверждает, что распределение получается более равномерным, если m является простым числом.
В рассмотренных примерах хеш-функция i = h(key) только определяет позицию, начиная с которой нужно искать (или первоначально – поместить в таблицу) запись с ключом key. Поэтому схема хеширования должна включать алгоритм решения конфликтов, определяющий порядок действий, если позиция i = h(key) оказывается уже занятой записью с другим ключом.
Схемы хеширования
В большинстве задач два и более ключей хешируются одинаково, но они не могут занимать в хеш-таблице одну и ту же ячейку. Существуют два возможных варианта: либо найти для нового ключа другую позицию, либо создать для каждого индекса хеш-таблицы отдельный список, в который помещаются все ключи, преобразованные в этот индекс.
Эти варианты и представляют собой две классические схемы:
– хеширование методом цепочек (со списками), или так называемое многомерное хеширование – chaining with separate lists;
– хеширование методом открытой адресации с линейным опробыванием – linear probe open addressing.
Метод открытой адресации с линейным опробыванием.Изначально все ячейки хеш-таблицы, которая является обычным одномерным массивом, помечены как не занятые. Поэтому при добавлении нового ключа проверяется, занята ли данная ячейка. Если ячейка занята, то алгоритм осуществляет осмотр по кругу до тех пор, пока не найдется свободное место («открытый адрес»), т.е. либо элементы с однородными ключами размещают вблизи полученного индекса, либо осуществляют двойное хеширование, используя для этого разные, но взаимосвязанные хеш-функции.
В дальнейшем, осуществляя поиск, сначала находят по ключу позицию i в таблице, и, если ключ не совпадает, то последующий поиск осуществляется в соответствии с алгоритмом разрешения конфликтов, начиная с позиции i по списку.
Метод цепочек используется чаще предыдущего.В этом случае полученный хеш-функцией индекс i трактуется как индекс в хеш-таблице списков, т.е. ключ key очередной записи отображается на позицию i = h(key) таблицы. Если позиция свободна, то в нее помещается элемент с ключом key, если же она занята, то отрабатывается алгоритм разрешения конфликтов, в результате которого такие ключи добавляются в список, начинающийся в i-й ячейке хеш-таблицы. Например, обозачив N –NULL:
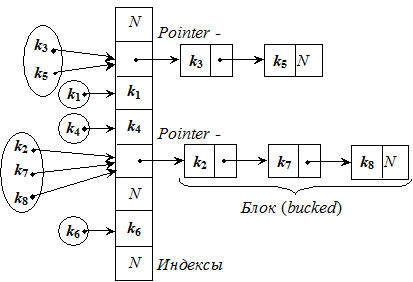
В итоге имеем таблицу массива связных списков или деревьев.
Процесс заполнения (считывания) хеш-таблицы прост, но доступ к элементам требует выполнения следующих операций:
– вычисление индекса i;
– поиск в соответствующей цепочке.
Для улучшения поиска при добавлении нового элемента можно использовать алгоритма вставки не в конец списка, а – с упорядочиванием, т.е. добавлять элемент в нужное место.
При решении задач на практике необходимо подобрать хеш-функцию i = h(key), которая по возможности равномерно отображает значения ключа key на интервал [0, m–1], m – размер хеш-таблицы. И чаще всего, если нет информации о вероятности распределения ключей по записям, используя метод деления, берут хеш-функцию i = h(key) = key%m.
При решении обратной задачи – доступ (поиск) к определенному подмножеству возможен из хеш-таблицы (хеш-структуры), которая обеспечивает по хеш-адресу (индексу) быстрый доступ к нужному элементу.
Дата добавления: 2016-01-09; просмотров: 3988;
