Ведомость вычисления высот точек съемочного обоснования

Номер точки	Длина линии d, м	Превышение h, м	Отметки H, м
hпр	hобр	hср	hиспр
	68,74   64,03   80,66   94,84   78,24   100,44   104,18   110,05	1,16   1,60   -0,13   1,10   -1,44   -1,48   3,35   -0,29	-1,17   -1,62   +0,15   -1,13   +1,42   +1,52   -3,39   0,33	+0,0042 1,16 +0,0043 1,61 +0,0042 -0,14 +0,0043 +1,12 +0,0042 -1,43 +0,0043 -1,50 +0,0042 3,37 +0,0043 -0,32	+1,164   +1,614   -0,136   +1,124   -1,426   -1,496   +3,374   -0,316	134,134   135,298   136,912   136,776   137,900   136,474   134,978   138,352   138,038
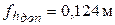
-	701,18	Σhср=3,87 Σhтеор=3,904 fh=-0,034	3,904	-

Уравнивание выполняют в следующей последовательности

Высотную невязку вычисляют как разность суммы практических (средних) превышений и теоретической суммы превышений:

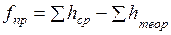. (1.35)

Для определения 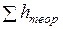для нивелирного хода, опирающегося на репера с известными отметками, запишем

;

;

;

..……………………

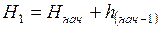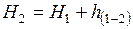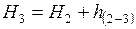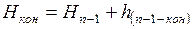. (1.36)

Сложив правые и левые части равенств, получим

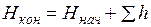, (1.37)

отсюда

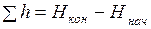. (1.38)

Так как отметки начальной и конечной точек являются исходными, т.е. безошибочными, последнее выражение можно использовать для вычисления теоретической суммы превышений:

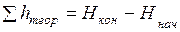. (1.39)

Итак, теоретическая сумма превышений в нивелирном ходе равна разности отметок конечного и начального реперов. Для нашего примера .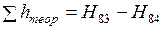

Отсюда высотная невязка для разомкнутого хода

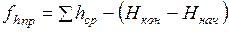. (1.40)

Если вычисленная невязка не превышает величины допустимой невязки, то ее (невязку) распределяют с обратным знаком поровну на все средние превышения и вычисляют уравненные значения превышений,

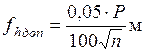; (1.41)

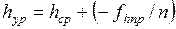, (1.42)

где n – число средних превышений.

При этом должно выполняться условие

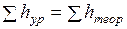. (1.43)

Затем вычисляют высоты всех связующих точек от высоты начального репера по уравненным превышениям:

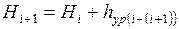. (1.44)

Контролем является получение в результате вычислений заданной высоты конечного репера.

Отметки реперов берутся из исходных данных (раздел 1.2).