Таким образом, имеем
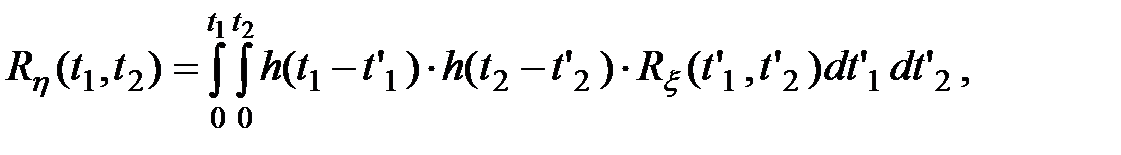 (4.13)
(4.13)
где
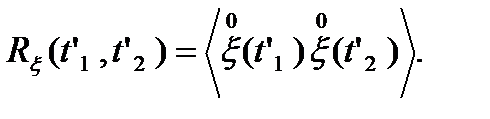
Из формулы (4.13) следует, что корреляционная функция выходного процесса определяется как двойная свертка между импульсной характеристикой цепи и корреляционной функцией входного процесса.
Если процесс  (t) стационарный, для которого
(t) стационарный, для которого
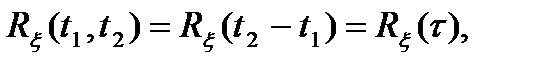
то при t1 = t и t2 = t + τ из формулы (4.13) имеем
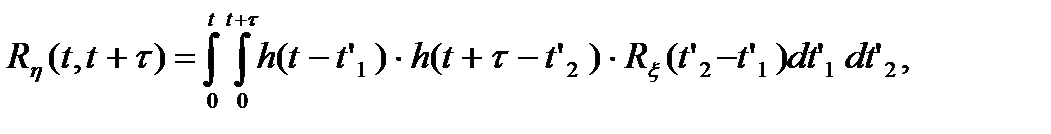 (4.14)
(4.14)
Заметим, что R (t, t + 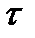 ) зависит от t и t +
) зависит от t и t + 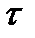 ; даже в случае, если
; даже в случае, если 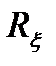 (t2 – t1) зависит только от их разности
(t2 – t1) зависит только от их разности 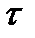 = t2 – t1 . Из этого следует, что в общем случае при включении на вход стационарного процесса выходной, из-за наличия переходного процесса, является не стационарным.
= t2 – t1 . Из этого следует, что в общем случае при включении на вход стационарного процесса выходной, из-за наличия переходного процесса, является не стационарным.
При 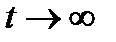 процесс
процесс  (t) становится стационарным. В этом случае корреляционная функция выходного процесса может быть определена при вычислении предела
(t) становится стационарным. В этом случае корреляционная функция выходного процесса может быть определена при вычислении предела
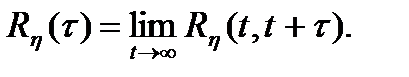 (4.15)
(4.15)
Практически выражения (4.8) и (4.15) становятся справедливыми раньше, чем при 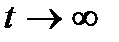 , именно после затухания переходных процессов. Например, стационарность выходного процесса по математическому ожиданию в случае цепи первого порядка достигается при
, именно после затухания переходных процессов. Например, стационарность выходного процесса по математическому ожиданию в случае цепи первого порядка достигается при 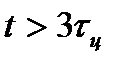 , где
, где 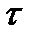 постоянная времени цепи, а по корреляционной функции из-за того, что берется двойная свертка, стационарность процесса достигается в два раза раньше, при
постоянная времени цепи, а по корреляционной функции из-за того, что берется двойная свертка, стационарность процесса достигается в два раза раньше, при 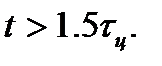
Дата добавления: 2016-01-26; просмотров: 829;
