Основные статистические модели сигналов и помех
В дальнейшем при решении отдельных задач статистической теории радиотехнических систем будем использовать следующие частные модели сигналов:
1. Детерминированный сигнал, то есть сигнал с полностью известными параметрами
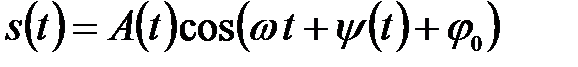 . (3.36)
. (3.36)
Его удобно использовать для получения потенциальных (предельных) характеристик оптимальных приемников.
2. Сигнал со случайной начальной фазой
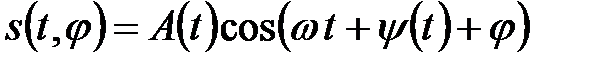 . (3.37)
. (3.37)
Здесь начальная фаза j принимаемого сигнала полагается случайной величиной с равномерным законом распределения (3.35) на интервале [- p, p].
3. Сигнал со случайными амплитудой и начальной фазой
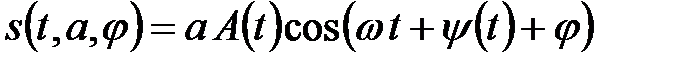 . (3.38)
. (3.38)
При этом начальная фаза j, по-прежнему, распределена равномерно на интервале [- p, p], а амплитуда a распределена по рэлеевскому закону (3.34).
Сигналы, описываемые детерминированными функциями, в которых один или несколько параметров являются случайными величинами, называют квазидетерминированными.
Для помех используют статистическое описание, включающее многомерные законы распределения. Требуемое статистическое описание помехи зависит от конкретной задачи. Часто достаточным является знание корреляционной функции помехи Rп(t) или спектральной плотности Sп(w).
Одномерную плотность распределения вероятностей мгновенных значений n(t) помехи очень часто полагают гауссовской
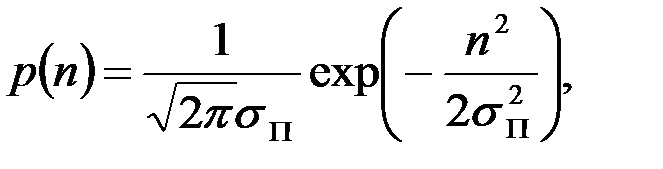 (3.39)
(3.39)
где 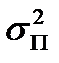 - дисперсия помехи, равная средней мощности флуктуаций помехи. При постоянной спектральной плотности шума N0 в пределах полосы от 0 до F дисперсия
- дисперсия помехи, равная средней мощности флуктуаций помехи. При постоянной спектральной плотности шума N0 в пределах полосы от 0 до F дисперсия 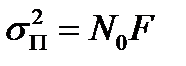 (рис. 3.5).
(рис. 3.5).
| N0 |
| w |
| Sп(w)) |
Dn= 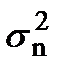 =N0Dw =N0Dw
|
|
| Rn(t) |
| Dw |
| t |
а) б)
Рис. 3.5
Шум, представляющий собой квазигармонический процесс с гауссовским законом распределения (3.39) мгновенных значений, имеет равномерный закон распределения (3.35) начальных фаз на интервале [-p, p], а огибающая Ап(t) для фиксированного момента t подчиняется рэлеевскому закону (3.34).
Для упрощения решения задач оптимального приема в качестве модели помехи вместо гауссовского шума часто используют белый шум. Спектральная плотность белого шума постоянна в неограниченной полосе частот и равна N0/2. Физическая спектральная плотность в полосе частот от 0 до ¥ равна N0 (рис. 3.6). Белый шум имеет корреляционную функцию
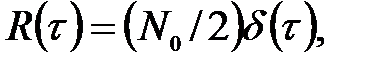 (3.40)
(3.40)
где d(t) - дельта - функция, равная нулю при t¹0 и обращающаяся в бесконечность при t = 0. Корреляционной функции (3.40) соответствует спектральная плотность шума Sп(w) = N0/2. Математическое ожидание белого шума <n(t)> считается равным нулю.

Рис. 3.6
Таким образом, при решении задач синтеза будем предполагать, что полезный сигнал s(t, 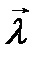 ) принимается на фоне аддитивного белого шума n(t) со следующими характеристиками:
) принимается на фоне аддитивного белого шума n(t) со следующими характеристиками:
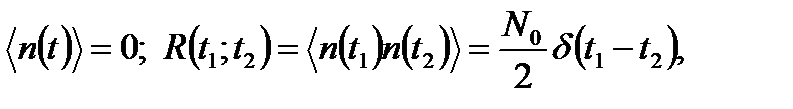 (3.41)
(3.41)
где угловые скобки означают операцию вычисления математического ожидания.
Для гауссовского белого шума в качестве n-мерной плотности вероятности можно использовать функционал плотности вероятности вида
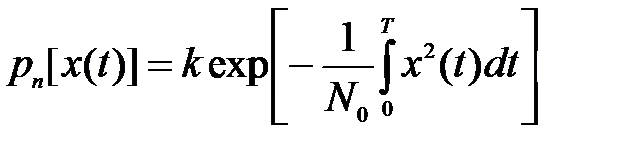 , (3.42)
, (3.42)
где k – коэффициент нормировки.
Хотя белый шум является абстрактной математической моделью, он широко используется в теоретических расчетах при исследовании узкополосных радиотехнических цепей, когда на них действует широкополосный шум, имеющий в полосе пропускания цепи постоянную спектральную плотность. Именно к такому виду задач сводится воздействие широкополосного шума транзисторов, ламп, сопротивлений на узкополосные радиотехнические цепи. В этом случае использование белого шума позволяет получить достаточно просто необходимые расчетные формулы.
Дата добавления: 2016-01-26; просмотров: 2463;
