Спектральная плотность стационарного случайного процесса
Спектральной плотностью стационарного случайного процесса 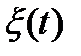 называется функция частоты
называется функция частоты 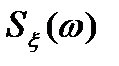 , являющаяся прямым преобразованием Фурье от корреляционной функции этого процесса
, являющаяся прямым преобразованием Фурье от корреляционной функции этого процесса
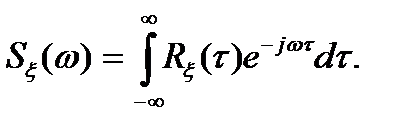 (3.12)
(3.12)
Если существует прямое (3.12) преобразование, то существует и обратное преобразование Фурье, которое по известной 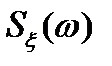 определяет
определяет 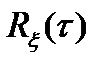 :
:
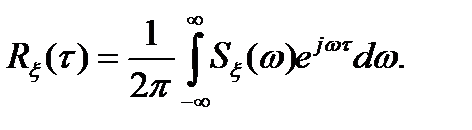 (3.13)
(3.13)
Формулы (3.12) и (3.13) принимают симметричный характер, если вместо круговой частоты w использовать частоту f. При этом 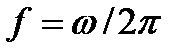 , а
, а 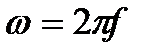 . Тогда имеем:
. Тогда имеем:
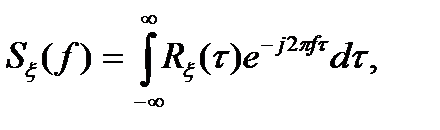 (3.14)
(3.14)
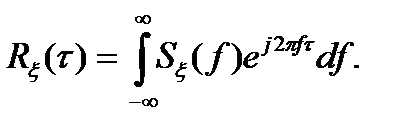 (3.15)
(3.15)
Воспользовавшись выражением (3.15), дадим физический смысл 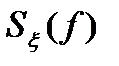 . Положив
. Положив 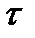 =0, получим
=0, получим
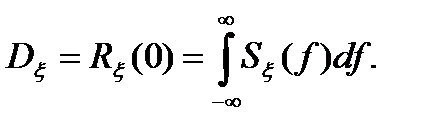 (3.16)
(3.16)
Как известно, 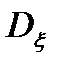 определяет среднюю удельную мощность флюктуаций случайного процесса. Поэтому функция частоты
определяет среднюю удельную мощность флюктуаций случайного процесса. Поэтому функция частоты 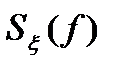 , от которой берется интеграл по всем частотам, в результате чего находится
, от которой берется интеграл по всем частотам, в результате чего находится 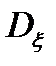 , характеризует среднюю мощность процесса, приходящуюся на единицу полосы частот. Размерностью
, характеризует среднюю мощность процесса, приходящуюся на единицу полосы частот. Размерностью 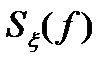 является размерность квадрата процесса, поделенная на размерность частоты. Если
является размерность квадрата процесса, поделенная на размерность частоты. Если 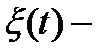 напряжение, то размерностью
напряжение, то размерностью 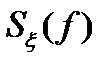 является [В2/Гц]. Заметим, что размерность
является [В2/Гц]. Заметим, что размерность 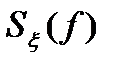 совпадает с размерностью энергии [В2/Гц] = [В2 С]. Поэтому в литературе
совпадает с размерностью энергии [В2/Гц] = [В2 С]. Поэтому в литературе 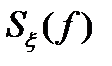 иногда называют энергетическим спектром.
иногда называют энергетическим спектром.
Рассмотрим основные свойства спектральной плотности 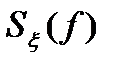 случайного процесса.
случайного процесса.
1. Спектральная плотность стационарного случайного процесса является действительной неотрицательной функцией частоты:
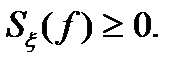 (3.17)
(3.17)
Это свойство вытекает из физического смысла 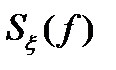 , определяющей средний квадрат флюктуаций в единичной полосе частот. Для действительного процесса
, определяющей средний квадрат флюктуаций в единичной полосе частот. Для действительного процесса 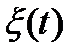 - средний квадрат флюктуаций есть всегда положительное число.
- средний квадрат флюктуаций есть всегда положительное число.
2.. Спектральная плотность стационарного процесса является четной функцией частоты:
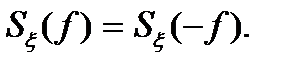 (3.18)
(3.18)
Это свойство обусловлено тем, что преобразование Фурье от четной функции, каковой является 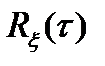 , есть, в свою очередь, четная функция.
, есть, в свою очередь, четная функция.
3. Пару преобразований Фурье, связывающую между собой спектральную плотность и корреляционную функцию, можно записать в виде косинус-преобразования. Используя это свойство, запишем выражения (3.12), (3.13) и (3.14), (3.15) в виде:
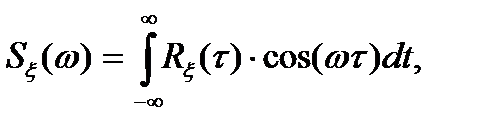 (3.19)
(3.19)
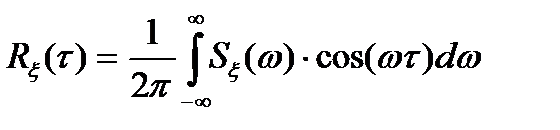 (3.20)
(3.20)
и
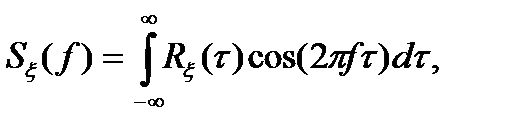 (3.21)
(3.21)
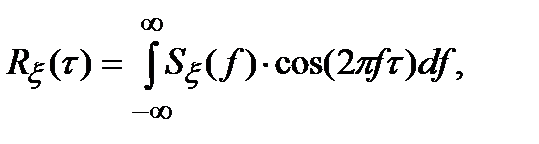 (3.22)
(3.22)
Формулы (3.19), (3.20) и (3.21), (3.22) называются формулами Винера - Хинчина по фамилиям ученых, которые впервые их получили.
4. Реальные радиотехнические устройства не различают знак частоты. Два колебания с одинаковой амплитудой и частотами, отличающимися только знаком, всегда воспринимаются устройством, как одно колебание с положительной частотой, но с удвоенной амплитудой.
Поэтому если 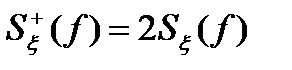 - спектральная плотность, определенная на
- спектральная плотность, определенная на 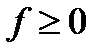 , а
, а 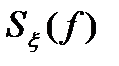 по-прежнему определена на всей оси частот от
по-прежнему определена на всей оси частот от 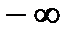 до
до 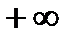 , то имеет место формула
, то имеет место формула
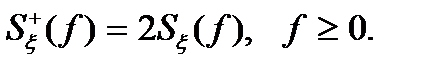 (3.23)
(3.23)
Спектральную плотность 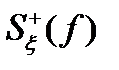 , определенную на
, определенную на 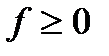 , будем называть физическим спектром, а спектральную плотность
, будем называть физическим спектром, а спектральную плотность 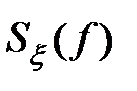 , определенную на
, определенную на 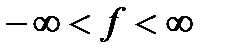 , - математическим спектром случайного процесса.
, - математическим спектром случайного процесса.
Формулы Винера-Хинчина для 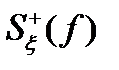 запишутся в виде:
запишутся в виде:
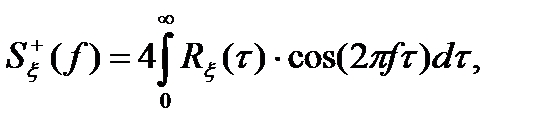 (3.24)
(3.24)
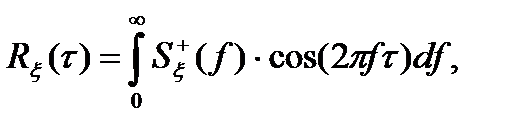 (3.25)
(3.25)
На рис. 3.2 показана связь между 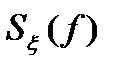 и
и 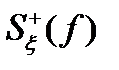 для случая низкочастотного широкополосного (рис. 3.2,а) и высокочастотных узкополосных процессов (рис. 3.2,б).
для случая низкочастотного широкополосного (рис. 3.2,а) и высокочастотных узкополосных процессов (рис. 3.2,б).

Рис. 3.2
5. Ширина 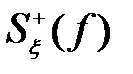 оценивается эффективной шириной спектра
оценивается эффективной шириной спектра 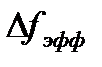 :
:
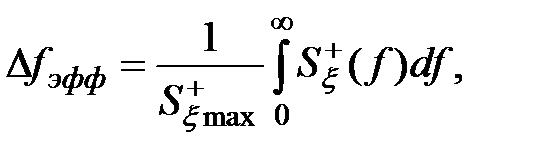 (3.26)
(3.26)
которая определяет основание прямоугольника с высотой 1, имеющего ту же площадь, что и фигура, ограниченная кривой 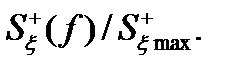
Дата добавления: 2016-01-26; просмотров: 2409;
