Стационарные и нестационарные случайные процессы

Стационарным случайным процессом в узком смысле называется случайный процесс, у которого n-мерная плотность вероятности не изменится, если все отсчеты времени сместить на одну и ту же величину:

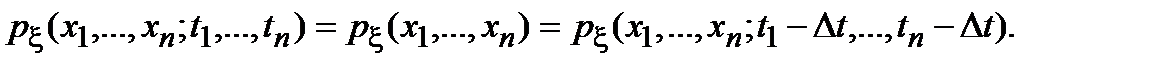(2.7)

Если выбрать 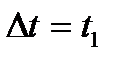, то n-мерная плотность вероятности не будет зависеть от начала отсчета времени

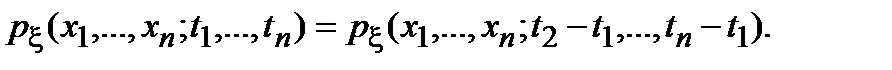(2.8)

Таким образом, для стационарного процесса одномерная плот­ность вероятности вообще не зависит от времени, а двумерная плот­ность зависит не в отдельности от t₁ и t₂ , а от их разности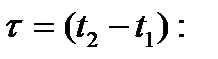

(2.9)

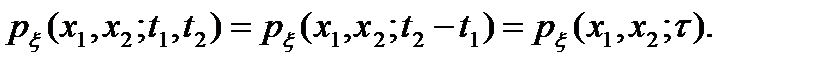(2.10)

В свою очередь, из выражений (2.9) и (2.10) вытекает, что математическое ожидание и дисперсия стационарного процесса не зависят от времени, а корреляционная функция зависит от t:

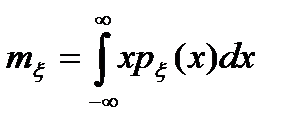(2.11)

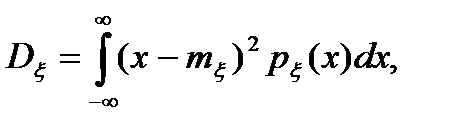(2.12)

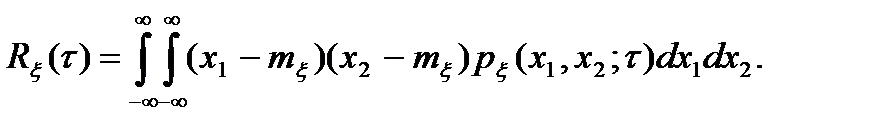(2.13)

Из (2.11), (2.12) и (2.13) следует, что математическое ожи­дание 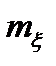постоянно и поэтому для стационарного процесса характе­ризует постоянную составляющую процесса; постоянность 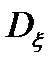харак­теризует то, что в каждой точке времени t средняя удельная мощность флюктуаций (то есть мощность переменной составляющей) одна и та же; зависимость 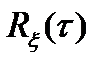от 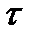означает, что для стационарного процесса неважно, в каких точках t₁ и t₂ берутся сечения, важна разность между ними .

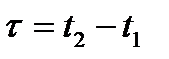Если условие (2.7) не выполняется, то случайный процесс на­зывается нестационарным. Иногда о стационарности судят только по выполнению равенств (2.9), (2.10) и, соответ­ственно, (2.11) - (2.13). Говорят, что, если выполняются равенства (2.9) и (2.10), то процесс является стационарным, не интересуясь при этом, выполняется условие (2.7) или нет. Такой подход дает более широкое толкование стационарности.

Определение стационарного процесса в широком смысле является более приемлемым для решения практических задач, так как проще получать данные об одномерной и двумерной плотностях вероятнос­ти, чем о многомерной.

В строгом смысле физически не существует стационарных слу­чайных процессов, так как любой процесс должен начаться в опреде­ленный момент времени в прошлом и, вероятно, завершиться в неко­торый момент в будущем. Однако есть много физических ситуаций, когда статистические характеристики процесса не изменяются на интервале времени наблюдения. В этих случаях предположение о стационарности приводит к удобной математической модели, которая является достаточно точной аппроксимацией реальной ситуации.