Способы описания случайных процессов

Существуют два способа представления случайных процессов. Во первых, случайный процесс представляется в виде совокупности или ансамбля всех своих возможных реализаций. То, какая конкретно реализация будет наблюдаться в испытании, является случайным событием. На рис. 2.2,а показан случайный процесс 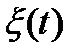, в ансамбль которого входят три реализации x₁(t)_, x₂(t), x₃(t), наблюдаемые в испытании с определенными вероятностями. Во вторых, случайный процесс 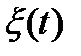рассматривается как n-мерная случайная величина или n-мерный вектор ( 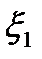, ,..., 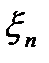), каждая проекция которого является отсчетом случайного процесса в моменты времени t₁,t₂,...,t_n (рис.2.2,б). Эти проекции вектора или отсчеты процесса будем называть сечениями случайного процесса:

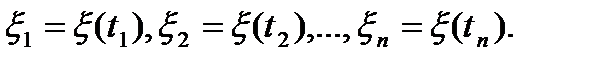(2.1)

Сечения (2.1) являются случайными величинами, так как из-за случайного выбора реализации их конкретные значения до опыта неизвестны. На рис. 2.2. пунктиром показан возможный ход случайного процесса и соответственно случайные величины 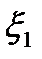, ,..., 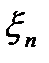на осях возможных значений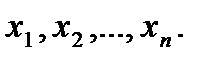

При достаточно большом п задание процесса n-мерным вектором эквивалентно заданию самого процесса. В теории случайных процес­сов доказывается, что для используемых на практике процессов чис­ло n конечно. Этот вывод базируется на том, что реализации слу­чайного процесса имеют ограниченную ширину спектра.

Рис. 2.2

Представление случайного процесса n-мерным вектором позволя­ет свести вероятностное описание процесса к описанию n-мерной случайной величины. Рассмотрим функцию распределения, плотность вероятности и числовые характеристики непрерывного случайного процесса, представленного n-мерным вектором.

В соответствии с этим n-мерная функция распределения случайного процесса 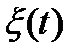определится выражением

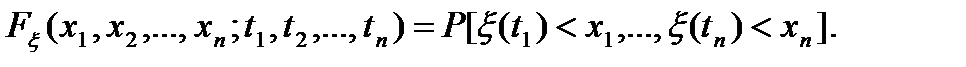(2.2)

Выражение (2.2) показывает, что в общем случае 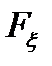зависит от 2n аргументов: от n наперед заданных возможных значений сечений ( 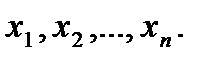) и от п моментов времени (t₁, t₂, ..., t_n), в ко­торых эти сечения берутся.

Многомерная плотность вероятности по определению равна част­ной производной n-го порядка от функции распределения по возможным значениям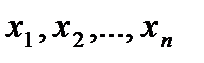

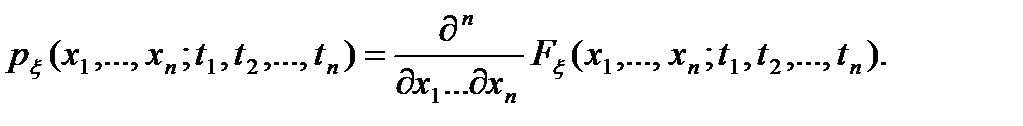(2.3)

Плотность вероятности n-го порядка в общем случае также зависит от тех же 2п аргументов. Произведение двумерной плотности вероятности на dx₁dx₂

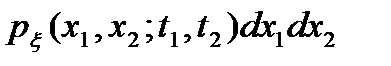
характеризует вероятность того, что реализация x(t) случайного процесса в моменты времени t₁, t₂ пройдет через интервалы 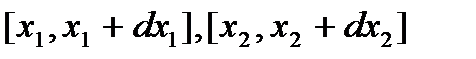. Это означает, что двумерная плотность вероятности содержит сведения о связи между двумя сечениями слу­чайного процесса, проведенными в моменты t₁ и t₂.

Одномерная плотность вероятности , где х₁ = х, t₁ = t определяет закон распределения случайной величины, полученной в результате сечения случайного процесса в момент t₁= t. Индекс 1 у времени и возможного значения здесь опускается, потому что сечение одно и надобность в индексе отпадает.

Представление случайного процесса n-мерным вектором позволя­ет получить такие числовые характеристики случайного процесса, как математическое ожидание, дисперсия, корреляционная функция. Эти характеристики, являющиеся соответственно начальными момента­ми первого порядка, центральным моментом второго порядка, смешан­ным центральным моментом второго порядка, зависят от моментов вре­мени, в которые берутся сечения случайного процесса, и поэтому являются моментными функциями времени.

Математическое ожидание и дисперсия 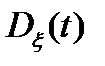требуют для своего определения использование одномерной плотности вероятности:

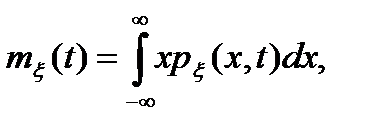(2.4)

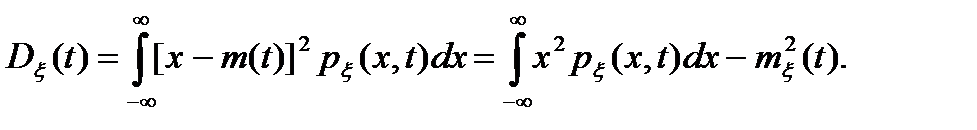(2. 5)

Для определения корреляционной функции требуется использование двумерной плотности вероятности

. (2.6)

Математическое ожидание определяет траекторию положения координаты центра тяжести одномерной плотности вероятности. Дисперсия 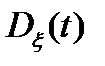характеризует изменение значения средней удельной мощности флуктуаций процесса во времени. Корреляционная функция 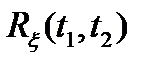характеризует случайный процесс с двух сторон: с одной стороны определяет среднею удельную мощность флуктуаций, а с другой – устанавливает степень линейной связи между сечениями случайного процесса, взятыми соответственно в моменты времени t₁ и t₂.