Корреляционная функция стационарного процесса

Корреляционная функция 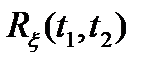слу­чайного процесса 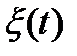определяется как математическое ожидание произведения двух центрированных сечений процесса, взятых в мо­менты t₁ и t₂. При этом математическое ожидание вычисляется с использованием двумерной плотности вероятности 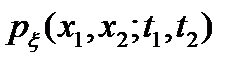. Для стационарного случайного процесса двумерная плотность вероятности и, соответственно, корреляционная функция зависят не от t₁ и t₂в отдельности, а только от их разности 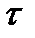= t₂ - t₁. В соответствии с этим корреляционная функция стационар­ного процесса определяется выражением

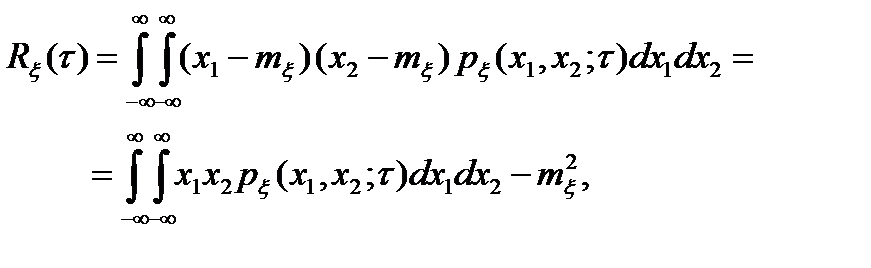(3.1)

где 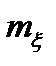- математическое ожидание стационарного процесса; х₁, х₂ - возможные значения случайного процесса соответственно, в моменты времени t₁, t₂ ; 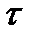= t₂ – t₁ - интервал времени между сечения­ми; 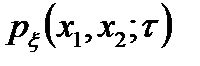- двумерная плотность вероятности стационарно­го процесса. Второе выражение для 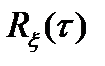получено путём раскрытия квадратных скобок первого выражения и учета свойств математичес­кого ожидания.

В научно-технической литературе используется также такая характеристика случайного процесса, как ковариационная функция K 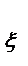(t), под которой понимается математическое ожидание произведения двух значений процесса, взятых соответ­ственно в моменты t₁ и t₂:

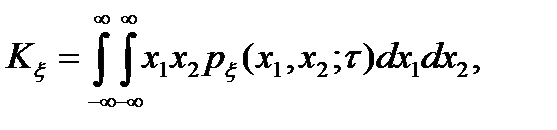(3.2)

так что справедливо соотношение

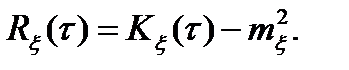(3.3)

Если 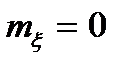, то понятия 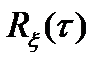и 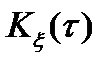совпадают. Если же до­полнительно 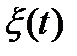обладает эргодическим свойством, то корреляцион­ная функция может быть определена по одной длинной реализации:

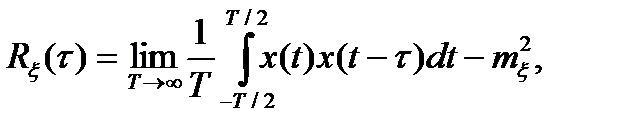(3.4)

где Т - интервал наблюдения единственной реализации x(t) процесса 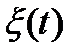; 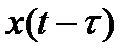- эта же реализация x(t), задержанная на время .

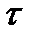Формула (3.4) может быть положена в основу построения Структурная схема уст­ройства, измеряющего корреляционную функцию, которое называется коррелометром. Для построения коррелометра требуются перемножитель, устройство задержки с переменным временем задержки 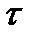и интегратор (рис. 3.1). Это устройство измеряет 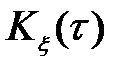или 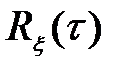в зависимости от того, равно 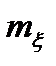нулю или нет.

Рис. 3.1

Корреляционная функция 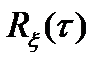стационарного случайного про­цесса, как и вообще корреляционная функция случайного процесса, является действительной функцией аргумента 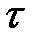. При этом 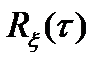характеризует 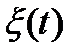с двух сторон. Во-первых, определяет среднюю удельную мощность флюктуаций. А во-вторых, позволяет судить о степени линейной связи между двумя сечениями случайного процесса, отстоящими друг от друга на интервал времени 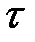. Размерность 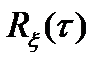совпадает с размерностью квадрата случайного процесса. Рассмотрим свойства корреляционной функции.

1. Корреляционная функция при 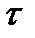= 0 равна дисперсии процесса

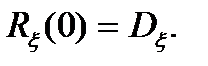(3.5)

Это свойство вытекает непосредственно из формулы (3.1), если в ней положить 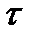= 0.

2. Корреляционная функция стационарного процесса является чётной функцией аргумента :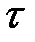

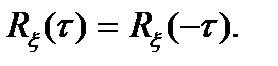(3.6)

Это свойство непосредственно вытекает из определения стационарно­го процесса, для которого важны не сами значения моментов 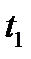и t₂, а расстояние во времени одного сечения от другого |t₂-t₁ |.

3. Корреляционная функция при любом t не может превзойти своего значения при 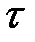= 0:

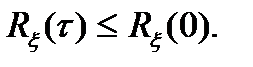(3.7)

Это свойство физически означает, что наибольшая степень линейной связи обеспечивается между одним и тем же сечением, то есть при 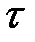=0. Правда, если 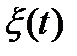является периодическим процессом, то может найтись еще какое-либо 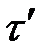, соизмеримое с периодом процесса, для которого выполняется жесткая функциональная связь между 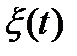и 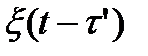. Поэтому в формуле (3.7) в общем случае может выполняться не только неравенство, но и равенство.

4. Корреляционная функция может быть представлена в виде

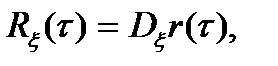(3.8)

где r(t) нормированная корреляционная функция, имеющая смысл коэффициента корреляции, зависящего от 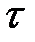и заключенная в пределах

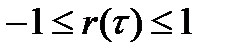. (3.9)

Она характеризует только степень линейной связи между сечениями слу­чайного процесса, взятыми через интервал 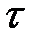. В свою очередь, дисперсия 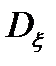процесса характеризует только среднюю удельную мощность флюктуаций случайного процесса.

5. Для широкого класса стационарных случайных процессов удовлетворяется условие

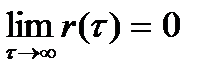. (3.10)

Физический смысл выражения (3.10) состоит в утверждении того фак­та, что линейная связь между сечениями случайного процесса при значительном удалении одного сечения от другого во времени отсут­ствует.

6. На практике важным параметром является интервал корреляции 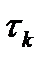, который характеризует эффективную ширину корреляционной функции. С общих позиций интервал корреляции опре­деляется выражением

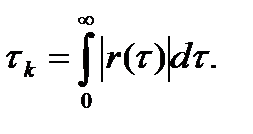(3.11)

Численно 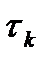равно основанию прямоугольника с высотой 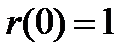, име­ющего ту же площадь, что и фигура, ограниченная криво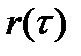й , при 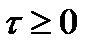. Интервал корреляции 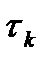определяет тот временной интервал между сечениями случайного процесса 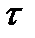, при превышении которого эти сечения считаются некоррелированными.