Эргодическое свойство стационарных случайных процессов

Среди всех стационарных процессов имеется часть, которая об­ладает эргодическим свойством. Поясним это свойство. Пусть имеется одна длинная реализация x(t) случайного процесса 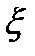(t). Эта реализация определена на интервале 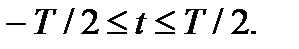Найдем среднее значение этой реализации путем ее усреднения во времени на достаточно большом интервале:

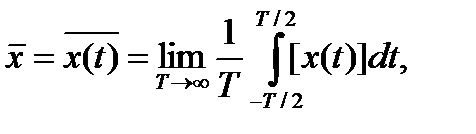(2.14)

где черта сверху означает усреднение по времени, среднее значение 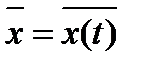является постоянной величиной, не зависящей от t.

Аналогично можно найти среднее значение квадрата флюктуаций и среднее значение произведения флюктуаций, смещенных одна отно­сительно другой на интервал :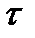

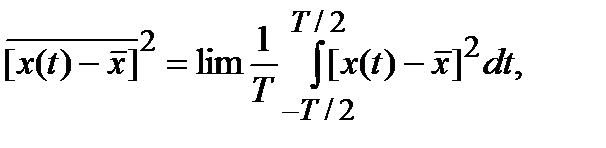(2.15)

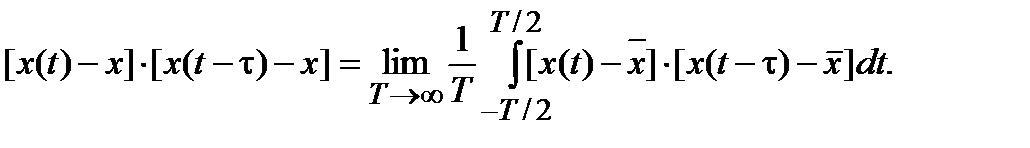(2.16)

По своему физическому смыслу величины (2.14) - (2.16) являются числовыми характеристиками, совпадающими со средним зна­чением, дисперсией и корреляционной функцией процесса 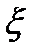(t). Одна­ко они получены в результате усреднения во времени одной длин­ной реализации x(t) или функции от нее.

Говорят, что стационарный процесс обладает эргодическим свойством, если с вероятностью, близкой к еди­нице, числовые характеристики, полученные в результате усреднения одной длинной реализации по времени, равны этим же характеристи­кам, полученным в результате усреднения по ансамблю. При этом ус­реднением по ансамблю называют определение числовых характеристик с использованием плотности вероятности, то есть по формулам (2.11) - (2.13), так как плотность вероятности характеризует всю совокупность или ансамбль реализаций.

Таким образом, для эргодического стационарного процесса справедливы равенства:

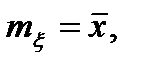
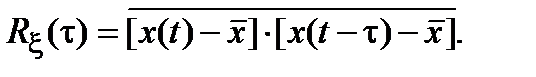, (2.17)

Само слово «эргодический»происходит от греческого «эргон», что означает «работа». Эргодическое свойство является удобной рабо­чей гипотезой для расчета числовых характеристик стационарного процесса, когда располагают одной длинной его реализацией. Физи­чески это обосновано тем, что одна длинная реализация может со­держать сведения обо всех реализациях этого случайного процесса.

Заметим, что стационарность процесса является необходимым, но недостаточным условием эргодичности. Это означает, что не все стационарные процессы являются эргодическими. В общем случае трудно, если только вообще возможно, дока­зать, что эргодичность - обоснованное допущение для какого-либо физического процесса, так как может наблюдаться только одна реа­лизация этого процесса. Тем не менее, обычно имеет смысл предполо­жить эргодичность процесса, если только отсутствуют веские доводы физического характера, препятствующие этому.