Условные плотности вероятности суммы сигнала и шума

В задаче обнаружения подлежащий наблюдению случайный процесс удобно записывать в виде суммы:

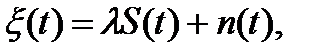(5.1)

где S(t) - детерминированный сигнал; n(t) - стационарный гауссовский шум с <n(t)> = 0, <n²(t)> = 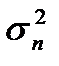; – случайная величина, равная 0, если сигнал отсутствует, и рав­ная 1, если присутствует.

Заметим, что процесс 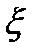(t), определяемый выражением (5.1), является случайным как из-за случайности шума n(t), так и из-за случайности величины 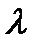. Последнее обстоятельство приводит к тому, что процесс (t) характеризуется условными плотностями вероятнос­тей: одной при условии, что 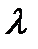= 0, а другой - при условии, что 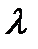= 1.

Если 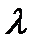= 0, то равенство (5.1) примет вид

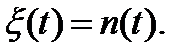(5.2)

В этом случае условная одномерная плотность вероятности определится в соответствии с формулой для гауссовского распределения с нулевым математическим ожиданием и диспер­сией 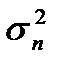выражением

(5.3)

где индекс n в 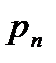(х) означает, что рассматривается плотность вероятности при условии, что 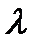= 0, когда действует только шум.

Если 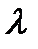= 1, то равенство (5.1) примет вид

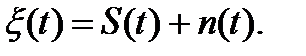(5.4)

При детерминированном сигнале процесс (5.4) будет иметь математическое ожидание, равное сигналу:

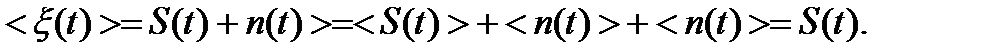(5.5)

В соответствии с этим условная плотность вероятности процес­са (5.4) будет определяться выражением, отличающимся от (5.3) только математическим ожиданием

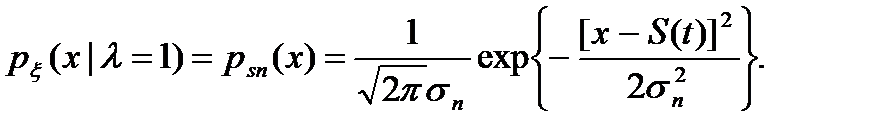(5.6)

Найдем условные n-мерные плотности вероятности в предположе­нии, что процесс 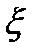(t) может наблюдаться на интервале времени [0,Т], а интервал времени корреляции шума равен 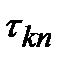. Если прово­дить сечение процесса через интервал 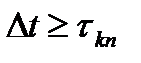, то все сечения

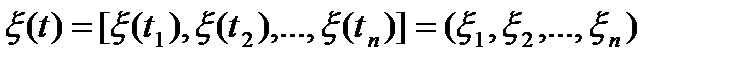(5.7)

будут некоррелированными, а та как процесс 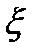(t) гауссовский, – независимыми. При этом число независимых сечений ограничивается величиной

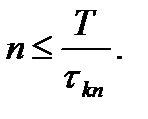(5.8)

Тогда условные n-мерные плотности вероятности определяются как произведения одномерных (5.3) или (5.6). Соответственно, для =0 и 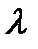= 1 эти плотности будут равны:

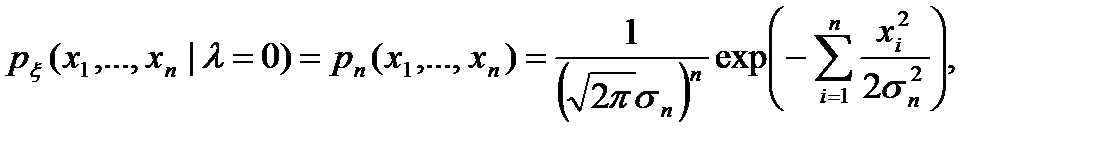(5.9)

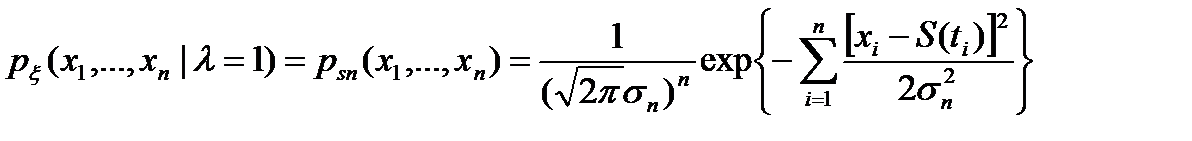(5.10)

где S(t_i) - значение сигнала S(t) в момент определения сечения t = t_i , i =1 ,2, . . ., n. .

Перейдём к непрерывному времени наблюдения, положив t₁ =0, t_n = Т. Если n(t) является гауссовским белым шумом, то согласно лекции №3 n-мерная плотность вероятности (5.9) превратится в ус­ловный функционал, в котором суммирование заменя­ется интегрированием, а последовательный ряд возможных значений (х₁, х₂, . . . ,х_n) вырождается в возможную реализацию x(t) :

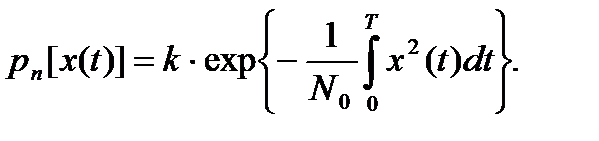(5.11)

Так как выражение (5.10) отличается от (5.9) только мате­матическим ожиданием, то при белом шуме плотность вероятности (5.10) переходит в условный функционал

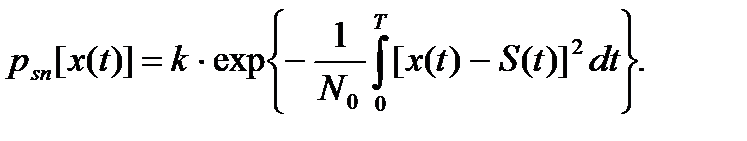(5.12)

Функционалы (5.11), (5.12) являются полными аналогами условных плотностей вероятности (5.9), (5.10), с той только разницей, что при решении практических задач ответы необходимо получать в виде отношения функционалов, чтобы коэффициент k, который при белом шуме стремится к нулю, сократился.

5.2.2 Функция правдоподобия при дискретном и непрерывном наблюдениях. Корреляционный прием

Выражения (5.9), (5.10) и (5.11), (5.12) можно рассматривать как условные плотности вероятности либо дискретной выборки (x₁,x₂,...x_n) объёма n, либо непрерывной выборки x(t), у которой мерой объёма является время наблюдения Т.

Задачу обнаружения можно свести к задаче оценки параметра . Если определить, что параметр 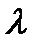=0, то в соответствии с (5.1) это то же самое, что принять решение о том, что в наблюдаемой реали­зации процесса 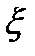(t) сигнал отсутствует. И наоборот, если определить, что 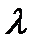= 1, то это значит принять решение о наличии сигнала S(t) в наблюдаемой реализации процесса (t).

Поэтому если в условные плотности вероятности (5.9), (5.10) поставить на место дискретных аргументов (х₁,х₂,...,х_n) конкретные результаты наблюдений ( 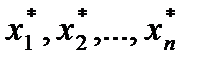), то получим функцию правдоподобия L( 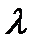) при диск­ретном наблюдении. При этом, так как параметр 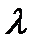может принимать только два значения, то и функция правдоподобия L( 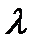) будет сос­тоять из двух значений:

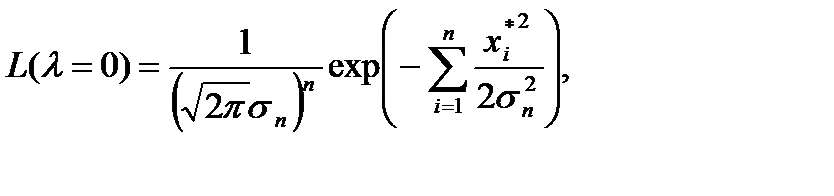(5.13)

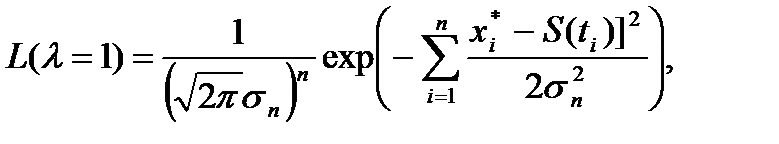(5.14)

Если же в условных функционалах (5.11), (5.12) на место возможной непрерывной реализации x(t) поставить конкретную зафик­сированную реализацию x*(t), получим функцию правдоподобия L( 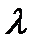) для непрерывного времени наблюдения, состоящую из двух значений L( 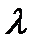= 0), L( 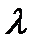= 1):

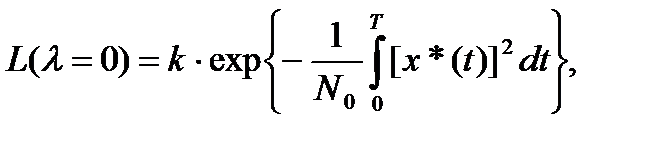(5.15)

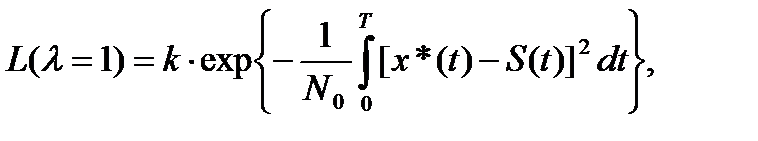(5.16)

В дальнейшем звездочки у 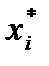и х*(t) в формулах для простоты написания будем опускать, но всегда будем иметь в виду, что в вы­ражениях для функции правдоподобия L( 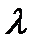) величины х_i и x(t) есть конкретные результаты наблюдений.

В задаче обнаружения при гауссовском шуме обычно используют­ся не сами значения функции правдоподобия L( 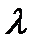=0) и L( 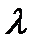=1), a логарифм их отношения 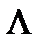. Найдем этот логарифм при непрерывном времени наблюдения:

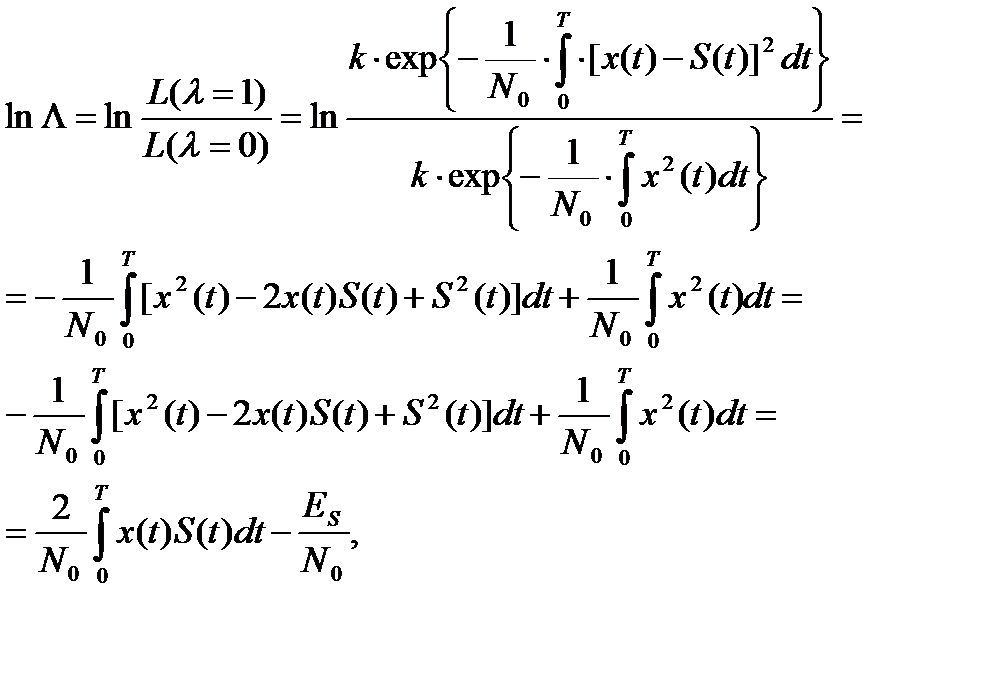(5.17)

где 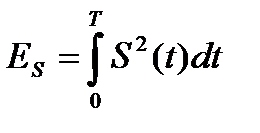- удельная энергия сигнала.

Полагаем, что отношение сигнал/шум по энергии при белом шуме определяется выражением .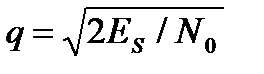

Тогда формулу (5.17) можно записать в виде

ln =ln 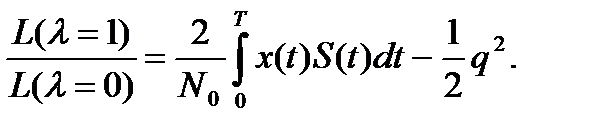(5.18)

Интеграл вида

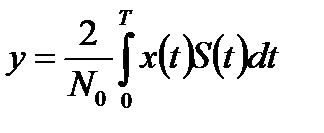(5.19)

называется взаимным корреляционным интегралом между наблюдаемым процессом x(t) и копией сигнала.

Математическая операция (5.19) является наиболее существен­ной для нахождения логарифма отношения правдоподобия, так как отношение сигнал/шум q для полностью известного сигнала и задан­ного уровня шума N₀ определено. В то же время (5.19) является функцией результата наблюдения x(t) и поэтому представляет собой статистику у. Учитывая, что статистика у полностью определяет логарифм отношения правдоподобия, её называют достаточной статистикой.

Радиоприёмник (рис. 5.1), реализующий вычисление взаимного корреляционного интеграла между наблюдаемым процессом x(t) и ко­пией сигнала S(t), называется корреляционным приёмником. Этот приёмник включает в себя гетеродин Г, воссоз­дающий копию сигнала S(t), перемножитель сигнала S(t) с входным процессом x(t) и интегратор. Результат вычислений получается на выходе интегратора в момент окончания наблюдения. Корреляционный приёмник лежит в основе построения многих оптимальных устройств, синтезируемых на основе решения оптимальных задач радиоприёма.

Рис. 5.1