По минимуму среднеквадратической ошибки

Оптимальным фильтром называется такое устройство, которое обеспечивает наилучшее по заданному критерию выделение сигнала из наблюдаемой смеси сигнала и шума. Смысл слова «выделение» сигнала совпадает с понятием оценки сигнала.

Пусть имеется сумма сигнала и шума:

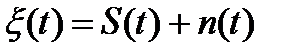(6.1)

где сигнал S(t) и шум n(t) являются стационарными случайными процессами с нулевыми математическими ожиданиями и корреляционными функциями R_s( 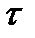) и R_n(t).

Рис. 6.1

Требуется, чтобы оценка сигнала 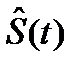, являющаяся откликом на воздействие 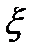(t) (рис. 6.1), была бы как можно ближе к истинному значению сигнала S(t). Тогда за ошибку фильтрации 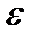(t) можно принять разность

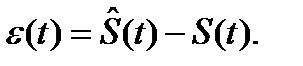(6.2)

Сделаем дополнительное предположение, что оценка сигнала 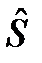(t) является стационарным случайным процессом. Тогда процесс 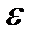(t) как разность двух стационарных процессов также будет стационарным. В этом случае удобно в качестве числовой характеристики ошибки 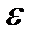(t) взять дисперсию

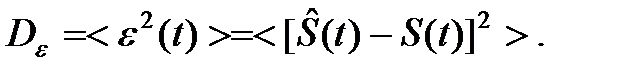(6.3)

Выберем за критерий оптимальности минимум дисперсии 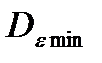. По этому критерию фильтр будет оптимальным в том случае, если он по сравнению с любыми другими фильтрами обеспечивает получение оценки сигнала 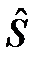(t) с наименьшим средним квадратом ошибки.

Если искать оптимальный фильтр среди линейных цепей с постоянными параметрами, то в качестве оценки 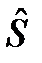(t) выступает выходной процесс

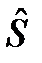
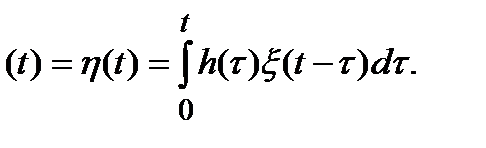(6.4)

Подставив (6.4) в (6.3), получим

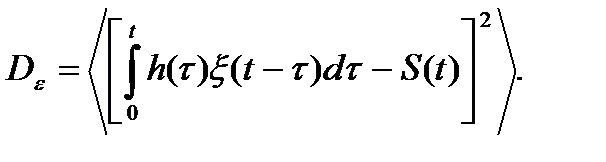(6.5)

Математическая задача нахождения оптимального фильтра сводится к отысканию такого вида импульсной характеристики фильтра h(t), при которой дисперсия (6.5) становится минимальной. Методами вариационного исчисления установлено, что искомая характе­ристика h(t) должна являться решением следующего интегрального уравнения:

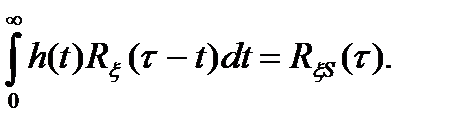(6.6)

где 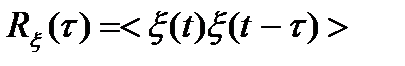- корреляционная функция процесса 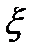(t) если S(t) и n(t) являются независимыми случайными процессами, то 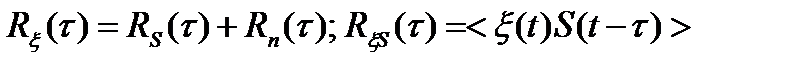– взаимная корреляционная функция между процессами 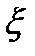(t) и S(t), для независимых S(t) и n(t) имеет место равенство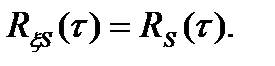

Уравнение (6.6) в научно-технической литературе называется уравнением Винера-Хопфа, а найденная из решения этого уравнения оптимальная импульсная характеристика h_opt(t)определяет оптимальный винеровский фильтр. Его комплексная частотная характеристика k_opt(j 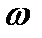) может быть найдена как преобразование Фурье от h_opt(t):

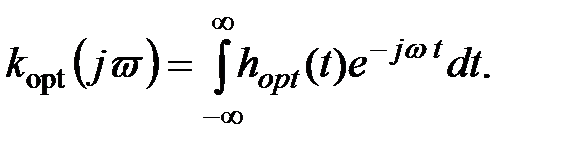(6.7)

Величина минимального квадрата ошибки винеровского фильтра определяется выражением

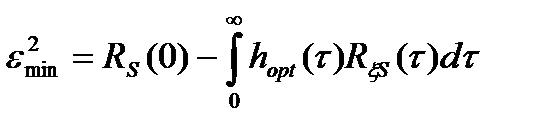. (6.8)

Однако следует заметить, что решение интегрального уравнения (6.6) наталкивается на значительные трудности даже в случае стационарности процессов 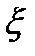(t) и S(t), когда для выработки оценки 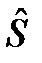(t) теоретически имеется все бесконечное прошлое процесса 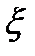(t), так как считается, что с момента воздействия 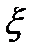(t) прошло значительное время и переходные процессы затухли. Сложность процедуры расчета h_opt(t) определяется как тем, что приходится решать интегральное уравнение, так и тем, что из всего класса решений h(t) требуется выбрать ту импульсную характеристику, которая удовлетворяет условию физической реализуемости, под которым понимается соотношение

h(t) = 0, если t < 0 .

Его смысл состоит в утверждении, что отклик линейной системы не может быть раньше воздействия. По этой причине рассмотренная процедура нахождения h_opt(t) и k_opt( 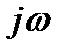) винеровского фильтра на практике не нашла широкого распространения.

В качестве примера рассмотрим k_opt( 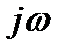) винеровского фильтра, полученного для процесса (6.1), в котором низкочастотный сигнал характеризуется корреляционной функцией и спектральной плотностью

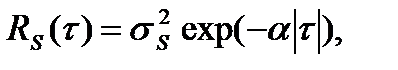
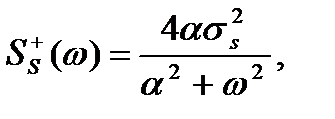(6.9)

где 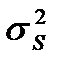- дисперсия сигнала; 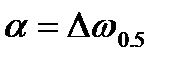- ширина спектра 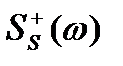на уровне 0.5, рад/с; 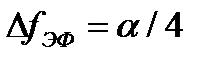- эффективная ширина спектра, Гц; n(t) - белый гауссовский шум с корреляционной функцией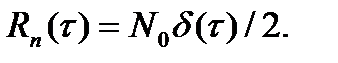

Процесс (6.1) с учетом (6.9) удобно характеризовать отно­шением сигнал/шум по мощности

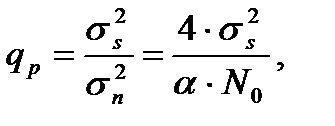(6.10)

где 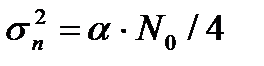- дисперсия шума в эффективной полосе спектра сигнала (6.9).

Отношение сигнал/шум (6.10) соответствует отношению мощности сигнала к мощности шума в эффективной полосе спектра сигнала.

Запишем без вывода найденную по рассмотренной выше процедуре комплексную частотную характеристику фильтра и ошибку фильтрации для этого случая

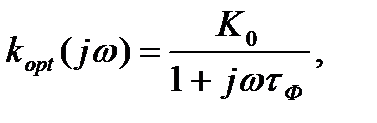(6.11)

где 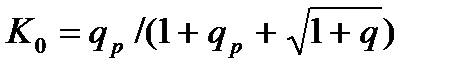- коэффициент передачи фильтра на нулевой частоте; 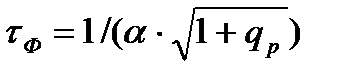постоянная времени фильтра;

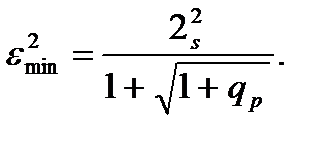(6.12)

Из (6.11) и (6.12) следует, что оптимальный винеровский фильтр для низкочастотного случайного сигнала (6.9) может быть реализован в виде простого интегрирующего RC - фильтра, у которого коэффициент передачи К_o и полоса пропускания зависят от отношения сигнал/шум. В частности, если q_р = 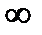(шум отсутствует), то К₀ = 1,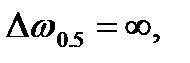 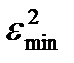=0, то есть при отсутствии шума никакой фильтрации осуществлять не надо и фильтр вырождается в устройство с коэффициентом передачи, равным единице. Если же 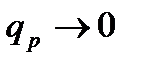а (полоса пропускания фильтра равна ширине спектра сигнала), коэффициент передачи стремится к нулю, К₀ 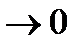. Это означает, что в качестве оценки сигнала берётся 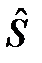(t) = 0. Средний квадрат ошибки при этом равен дисперсии сигнала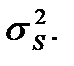

Таким образом, структура винеровского фильтра (зависимость h_opt(t) или k_opt( 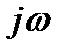)) определяется характеристиками сигнала и шума, а параметры фильтра и ошибки фильтрации зависят от отношения сигнал/шум.