Обнаружение сигналов как статистическая задача

Пусть на вход обнаружителя поступает сумма сигнала s(t) и шума n(t), представляющая собой случайный непрерывный процесс

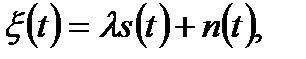(7.1)

где s(t) - полностью известный сигнал; l - случайный параметр, равный 1, когда сигнал присутствует, и равный 0, когда сигнал отсутствует; n(t) - шум с известным законом распределения.

Обнаружитель анализирует реализацию x(t) процесса x(t) в течение заранее выбранного (конечного) интервала времени Т и затем на основании анализа принимает решение: существует ли сигнал в наблюдаемой реализации или нет.

В настоящее время для решения подобных задач широко применяются методы математической статистики. Основной задачей математической статистики является установление законов распределения случайных величин на основе результатов наблюдения над этими величинами. В результате наблюдения над некоторой случайной величиной получается совокупность выборочных (x₁, ..., x_n) значений этой величины, называемая выборкой; число n выборочных значений, содержащихся в данной выборке, называется объемом выборки.

В случае обнаружения сигналов реализация x(t) является непрерывной функцией времени (при непрерывном или дискретном сигнале s(t) в смеси) с ограниченным спектром. Представим x(t) выборочными значениями (x₁, ..., x_n), взятыми в соответствии с теоремой Котельникова с интервалом Dt = 1/2F, где F - эффективная ширина спектра колебания x(t). При этом объем выборки определяется соотношением

n = T/ Dt = 2TF . (7.2)

На основании анализа выборки (x₁, ..., x_n) обнаружитель должен оценить параметр l. Очевидно точность оценки зависит от объема выборки при неограниченном времени наблюдения Т. Однако на практике Т ограничено, а с увеличением объема выборки при T = const погрешность оценки не устремляется к нулю.

Выборка, у которой n ® ¥ при T = const, называется непрерывной. Вид выборки (дискретная или непрерывная) определяется удобством математического анализа. Заметим, что если для дискретной выборки какая-либо формула получена в виде суммы, то соответствующий результат для непрерывной выборки может быть получен при замене суммы интегралом, если в этой формуле положить Dt ® 0 или n ® ¥ при T = const. Дискретизация проводится в соответствии с теоремой Котельникова: для дискретизации аналогового сигнала без потерь информации частота отсчетов должна быть в два раза выше верхней граничной частоты спектра сигнала.

Поскольку в задачах обнаружения оценка параметра l является дискретной (l = 0 или l = 1), при конечном объеме выборки можно лишь с некоторыми вероятностями высказать статистические гипотезы. Следовательно, решение задачи обнаружения сводится к проверке двух альтернативных (противоположных) статистических гипотез. Гипотеза Н₁ - сигнал во входной смеси есть (l = 1) и гипотеза Н₀ - сигнала нет (l = 0). При этом вероятности Р(Н₁) и Р(Н₀) являются соответственно априорными вероятностями наличия и отсутствия сигнала.