Дифференциальные уравнения конвективного теплообмена

Так как процесс конвективной теплоотдачи характеризуется совокупностью тепловых и гидродинамических явлений, то такой процесс в виде может быть описан системой дифференциальных уравнений, учитывающих как тепловые, так и гидродинамические яв­ления. В систему дифференциальных уравнений конвективного тепло­обмена входят: уравнение энергии, уравнение движения, уравнение сплошности, уравнение теплоотдачи (теплообмена).

1. Уравнение энергии.

Дифференциальное уравнение энергии описывает температурное поле в движущейся жидкости, т.е. устанавливает связь между прост­ранственным и временным изменением температуры в любой точке дви­жущейся жидкости.

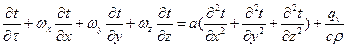(106)

Если скорости ω_x=ω_y=ω_z=0(например, для твердого тела), то уравнение энергии переходит в выведенное нами ранее уравнение теп­лопроводности (16).

Многочлен, стоящий в левой части уравнения (106), представ­ляет собой полную производную от температуры по времени, т.к. если t=f(τ, x, y, z), то на основании понятия о полной производной имеем:

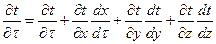
где , ,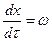

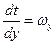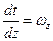
С учетом сказанного уравнение (106) запишется:

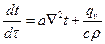(107)

2. Уравнение движения.

В общем случае трехмерного движения несжимаемой жидкости с постоянными физическими параметрами скоростное поле описывается уравнениями движения, каждое соответственно в проекциях сил на оси Ox, Oy, Oz:

для оcи Oх

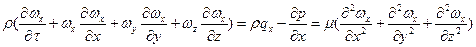(108)

для оси Oy:

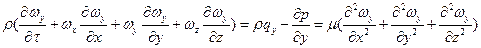(109) для оcи Oz:

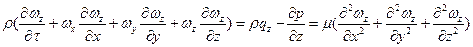(110)

Уравнения (108)-(110) называют уравнениями Навье-Стокса. Все слагаемые этих уравнений имеют размерность силы, отнесенной к едини­це объема.

3. Уравнение сплошности.

Уравнение сплошности или неразрывности для сжимаемых жидкостей имеет вид:

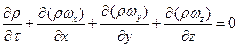(111)

Для несжимаемых жидкостей при ρ=const уравнение (111) запишется

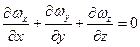(112)

Таким образом, уравнения энергии (106), движения (108),(109),(110) и сплошности (111) составляют систему уравнений, которая математически описывает процесс конвективного теплообмена для несжимаемой жидкости. Если искомой величиной является коэффициент теплоотдачи, то система должна быть дополнена дифференциальным уравнением теп­лоотдачи.

4. Уравнение теплоотдачи.

Это уравнение получено ранее в разделе теплопроводности

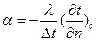(113)

Дифференциальные уравнения (106), (108)-(110),(111) и (112) описывают процесс теплоотдачи в самом общем виде. При решении кон­кретных задач конвективного теплообмена к системе указанных дифференциальных уравнений необходимо добавить условия однозначности. Условия однозначности задаются аналогично условиям однозначности в разделе теплопроводности, т.е. они включают в себя: геометрические, физические, начальные или временные и граничные условия.

Таким образом, конвективная теплоотдача описывается приведенной системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитическо­го решения этой системы уравнений наталкиваются на серьезные труд­ности. В настоящее время такое решение получено лишь для отдель­ных, наиболее простых задач процесса теплоотдачи и лишь при целом ряде упрощающих предпосылок. Поскольку эти предпосылки отличаются от действительных условий протекания процессов, то и полученные аналитические решения плохо согласуются с опытными данными. Тем не менее, наличие дифференциальных уравнений, описывающих конвективный теплообмен, необходимо и для других методов расчета конвективной теплоотдачи.