Основы теории подобия.

При изучении различных физических явлений применяют два мето­да исследований: экспериментальныйи теоретический(или метод ма­тематической физики). Достоинством экспериментального метода исследования является достоверность получаемых результатов. Основной недостаток экспериментального метода исследования заключается в том, что результаты данного эксперимента не могут бить использованы применительно к другому явлению, которое в деталях отличается от изученного. Следовательно, при экспериментальном методе каждый конкретный случай должен служить самостоятельным объектом изучения. Последнее обстоятельство является органическим недостатком экспе­риментального метода исследований.

Второй метод исследования для нахождения количественных зави­симостей широко применяется современной наукой и рассматривается в математической или теоретической физике. Суть этого метода состоит в том, что изучаемое физическое явление описывается дифференциальным уравнением (или системой уравнений), т.е. составляется математическая модель этого явлений. Так как при этих урав­нений используются самые общие законы природы, то дифференциальное уравнение (или система уравнений) является математической моделью целого класса явлений. Под классом понимается такая совокупность явлений, которая характеризуется одинаковым механизмом процессов и одинаковой физической природой. Для того, чтобы однозначно опи­сать единичное явление, входящее в класс явлений, необходимо к диф­ференциальному уравнению (или системе уравнений) добавить условия однозначности. В большинстве случаев и, в частности, при описании конвективного теплообмена из-за сложности изучаемых явлений найти решение, удовлетворяющее системе дифференциальных уравнений и усло­виям однозначности, невозможно. Следовательно, если недостатком экспериментального метода исследования является невозможность распространения результатов, полученных в данном опыте , на другие явления, отличающиеся от изученного, то недостатком математической физики является невоз­можность перейти от класса явлений, характеризуемых дифференциальными уравнениями и условиями однозначности, к конкретному единичному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.

Если положительные стороны математического и эксперименталь­ного методов исследования объединить в целое, то полу­чим универсальный аппарат изучения различиях явлений природа. Такое объединение обоих методов осуществляется теорией подобия.

Теория подобия - это учение о подобии явлений. Впервые с понятием подобия мы встречаемся в геометрии, откуда этот термин и заимствован. Как известно, геометрически подобные фигуры, напри­мер треугольники, обладают свойством, что их соответственные углы равны, а сходственные стороны пропорциональны, т.е.

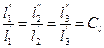(117)

где l₁', l₂', l₃'- линейные размеры одной фигуры;

l₁″, l₂″, l₃″- сходственнее линейные размеры другой фигуры;

C_l - константа геометрического подобия.

Условие (116) является математической формулировкой геометрического подобия.

Понятие подобия может быть распространено на любые физические явления. Можно говорить, например, о подобии движения двух потоков жидкости-кинематическом подобии; о подобии сил, вызывающих подобные между собой движения, динамическом подобии; о подобии распределения температур и тепловых потоков - тепловом подобии и т.п.

Для сложных физических явлений должны выполняться следующие условия подобия:

1) Понятие подобия в отношении физических явлений применимо только к явлениям одного и того же рода, которые качественно оди­наковы и описываются одинаковыми уравнениями, как по форме, так и по содержанию.

Если же математическое описание двух каких-либо явлений одинаково по форме, но различно по физическому содержанию, то такие явления называются аналогичными. Такая аналогия существует, напри­мер, между процессами теплопроводности, электропроводности и диффузии.

2) Обязательной предпосылкой подобия физических явлений долж­но быть геометрическое подобие, т.е. подобные явления всегда про­текают в геометрически подобных системах.

3) При анализе подобных явлений сопоставлять между собой мож­но только однородные величины и лишь в сходственных точках прост­ранства и в сходственные моменты времени.

Однородными называются такие величины, которые имеют один и тот же физический смысл и одинаковую размерность.

Сходственными точками геометрически подобных систем называ­ются такие точки, координаты которых удовлетворяют условию (116):

, ,

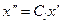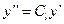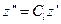
Два промежутка времени τ' и τ″ называются сходственными, если они имеют начало отсчета, и связаны преобразованием подобия, т.е. τ″=С_τ*τ'

4) Подобие двух физических явлений означает подобие всех ве­личин, характеризующих рассматриваемых явлений.

Это означает, что в сходственных точках пространства и в сходственные моменты времени любая величина φ' первого явления пропорциональна однородной с ней величине φ" второго явления, т.е.

φ"= С_φ*φ'

где С_φ- константа подобия (или множитель подобного преобразования).

При этом физическая величина имеет свою константу по­добия, например:

, , , ,

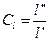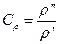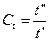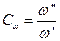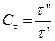
Приведенные константы подобия называют: линейная, плотностная, температурная, скоростная, временная.

Константы подобия для различных величин в подобных явлениях нельзя назначать или избирать произвольно. Между ними имеются строго определенные соотношения, которые выводятся из анализа математичес­кого описания процессов. Эти соотношения имеют центральное значение в теории подобия, так как они устанавливают существование особых величин, называемых числами или критериями подобия, которые для всех подобных между собой явлений сохраняют одно и то же числовое значение. Покажем это на примере. Для примера воспользуемся диффе­ренциальным уравнением теплоотдачи. Это уравнение для сходственных точек двух подобных систем запишется так:

для первой системы 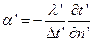(а)

для второй системы 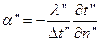(б)

Обозначим константы подобия:

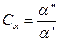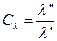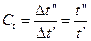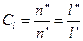, , , (в)

где l- характерный (определяющий) размер системы. Из уравнений (в) получаем:

, , , , ,

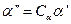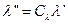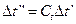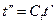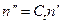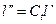
Подставив эти выражения в уравнение (б), получим

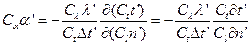
Сократив на С_t и разделив левую и правую часть на С_α, получим

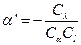(г)

Сравнивая (а) и (г), получим, что

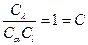(д)

Из уравнения (д) следует, что выбор комплекса констант подо­бия ограничен условием: любая их комбинация должна быть равна еди­нице. Величину С называют индикатором подобия.

Заменив значения констант подобия в уравнении (д) из уравнений (в), получаем:

,

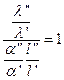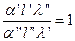
Умножив левую и правую часть последнего уравнения на α″*l″/λ″, получим

α'*l'/λ'=α″*l″/λ″

или в общем случа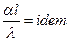е (е)

Такие комплексы величин называются числами подобия.

Числа подобия являются безразмерными комплексами, составлен­ными из разнородных физических величин, характеризующих данное явление. При этом нулевая размерность является характерным свойством числа подобия и может служить проверкой правильности его составле­ния. Числа подобия принято называть именами ученых, работающих в соответствующей области науки, и обозначать двумя начальными буквами их фамилий. Получают числа подобия из аналитических зависи­мостей, описывающих данный процесс. Таким образом, математические описания процесса, хотя бы в виде неинтегрируемых дифференциальных уравнений общего вида, является необходимой предпосылкой ис­пользования теории подобия. Это положение лежит в основе практи­ческого применения теории подобия.

Записанное уравнением (е) число называют числом Нуссельта и обозначают N_U. Равенство (е) можно представить в виде:

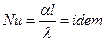
Для характеристики подобия явлений можно применять константы подобия и числа подобия. Но при этом нужно помнить, что константе подобия сохраняют числовое значение только для двух подобных явлений, оставаясь одинаковыми для всех сходственных точек рассматривае­мых систем. Числа подобия сохраняют свое числовое значение в сходственных точках всех подобных между собой систем, но в различных точках одной и той же системы они могут иметь разные числовые зна­чения.

Основные положения теории подобия обычно формулируются в виде теорем подобия.

Первая теорема подобия.

В подобных явлениях одноименные числа подобия в сходственных точках и в сходственные моменты временя имеют одинаковые числовые значения.

Вторая теорема подобия.

Зависимость между переменными величинами, характеризующими какое-либо явление, может быть представлена в виде зависимости между числами подобия.

Эта зависимость между числами подобия называется уравнением подобия (или критериальным уравнением).

Вторую теорему подобия можно сформулировать так:

если физическое явление описывается дифференциальным уравнением (или системой уравнений), то всегда существует возможность представить его (их) в виде уравнения подобия.

Третья теорема подобия отвечает на воп­рос, какие условия достаточны, чтобы явления были подобны.

Подобны те явления условия однозначности которых подобны, и числа подобия, составленные из условий однозначности в сходственных точках и сходственные моменты времени численно одинаковы.