Закон Ньютона-Рихмана. Коэффициент теплоотдачи.
В практических инженерных расчетах теплоотдачу, т.е. теплообмен между поверхностью твердого тела и движущейся средой, соприкасающейся с этой поверхностью, описывают законом Ньютона-Рихмана (20).
Согласно закону Ньютона-Рихмана тепловой поток Q от жидкости к стенке или от стенки к жидкости пропорционален поверхности теплообмена F и разности температур ∆t=(tc-tж) жидкости и стенки:
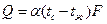 , [Вт] (114)
, [Вт] (114)
Разность температур (tc-tж) или (tж- tc) называют температурном напором.
Уравнение Ньютона-Рихмана для всего тепла Qτ, передаваемого за время τ запишется:
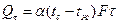 ,
, 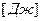 (115)
(115)
для плотности теплового потока:
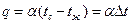 ,
, 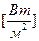 (116)
(116)
Уравнения (113)- (115) записаны для случая tc> tж. Если tж< tc, то в эти уравнения нужно записать tж - tc.
Коэффициент пропорциональности α, входящий в уравнение Ньютона-Рихмана, называется коэффициентом теплоотдачи. Он учитывает конкретные условия процесса теплоотдачи, влияющие на его интенсивность и имеет размерность:[α]=Вт/м2*К
Коэффициент теплоотдачи α характеризует интенсивность теплообмена на границе жидкость - стенка и численно равен количеству тепла, переданного в единицу времени через единицу поверхности, при разности температур между поверхностью и жидкостью в один градус. Коэффициент теплоотдачи α в отличие от коэффициента теплопроводности λ не является физическим параметром среды и зависит от многих факторов.
В общем случае коэффициент теплоотдачи может изменяться по поверхности теплообмена, и поэтому различают средний по поверхности и локальный или местный коэффициент теплоотдачи. Поэтому в общем случае с учетом переменности по поверхности уравнение Ньютона-Рихмана запишется:
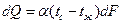 ,
,
отсюда 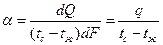
Последнее тождество можно рассматривать как определение α: коэффициент теплоотдачи есть плотность теплового потока на границе жидкость - стенка, отнесенная к разности температур стенки и жидкости. В соответствии с сказанным в уравнениях (113)-(115) под α следует понимать его среднее значение.
Применение формулы Ньютона-Рихмана никаких принципиальных упрощений для расчета конвективной теплоотдачи не дает. Вся сложность расчета в этом случае переносится на определение коэффициента теплоотдачи, т.е. простота формулы (113)-(115) является лишь кажущейся. В общем случае является функцией многих величин:
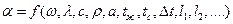
Т.е. в общем случае α является функцией скорости движения жидкости, режима движения, физических параметров жидкости, температуры жидкости и тела, формы и размеров омываемого тела и т.д.
Инженерное решение задач конвективного теплообмена сводится чаще всего к определению α и вычислению количества переданной теплоты по формулам (2.127)-(2.129). Так как определить коэффициент теплоотдачи путем аналитического решения, приведенной в предыдущем параграфе, системы дифференциальных уравнений достаточно сложно, а в некоторых случаях и вообще невозможно, то для расчета α применяют теорию подобия.
Дата добавления: 2016-01-18; просмотров: 2424;
