Числа подобия и уравнения подобия

Существует несколько методов получения чисел подобия. Метод получения чисел подобия, основанный на анализе соотношений между константами подобия, которые получаются из дифференциальных урав­нений (этот метод применен нами в §4 для получения числа Нуссель­та). Метод масштабных преобразований, в основе которого лежит приведение дифференциальных уравнений к безразмерному виду (при­мер такого преобразования рассмотрен в разделе нестационарной теплопроводности). Существуют и другие методы, например, метод размерностей.

При расчете конвективного теплообмена используется достаточ­но большое количество чисел подобия. Рассмотрим наиболее часто употребляемые числа подобия для расчета конвективной теплоотдачи однофазных потоков.

I. Число Нуссельта:

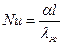
где α - коэффициент теплоотдачи, Вт/м²К; ℓ - определяющий (характерный) размер, м; λ_ж - коэффициент теплопроводности жид­кости, Вт/мК.

Число Нуссельта характеризует теплообмен на границе стенка-жидкость. Иногда число Нуссельта называют безразмерным коэффици­ентом теплоотдачи.

При рассмотрении нестационарной теплопроводности мы пользова­лись числом 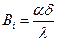. Несмотря на внешнее сходство, чис­ло N_U существенно отличается от числа B_i. В число B_i входит коэффициент теплопроводности твердого тела λ, а в число N_U - жидкости. Кроме того, в B_i коэффициент теплоотдачи α вводится как величина заданная, а в числе N_U α рассматривается как величина искомая.

2. Число Прандтля:

P_r = υ/α

где υ - кинематический коэффициент вязкости, м²/с, а - коэффициент температуропроводности жидкости, м²/с. Число Прандтля характеризует физические свойства жидкости. Поскольку число Прандтля составлено лишь из физических параметров, то можно ска­зать, что само оно является теплофизическим параметром жидкости. Обычно значения чисел Прандтля приводятся в таблицах. Отметим, что числа Прандтля капельных жидкостей сильно зависят от темпера­туры, числа P_r газов практически не зависят ни от температуры, ни от давления.

3. Число Пекле:

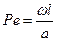
где ω - средняя скорость потока жидкости, м/с; ℓ- определяю­щий размер,м; а - коэффициент температуропроводности жидкости, м²с. В числе Пекле числитель характеризует теплоту, переносимую конвекцией, а знаменатель- теплоту, переносимую теплопроводностью. Т.е. число P_е характеризует отношение конвективного и молекулярно­го переноса тепла в потоке.

4. Число Рейнольдса:

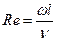
Число Рейнольдса характеризует соотношение сил инерции и сил вязкости при вынужденном движении жидкости, т.е. характеризует гидродинамический режим движения жидкости.

5. Число Грасгофа:

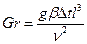
где g - ускорение свободного падения, м/с, β- коэффициент объемного расширения жидкости, I/к (в общем случае 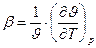для идеального газа β=1/Т); ∆t=t_c-t_ж - температурный напор между стенкой и жидкостью.

Число Грасгофа характеризует подъемные силы, возникающие в жидкости вследствие разности плотностей нагретых и холодных частиц жидкости, и связывает подъемные силы и силы вязкости. Можно сказать, что число Грасгофа характеризует свободное движение жидкости или свободную конвекцию.

6. Число Фурье:

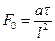
где τ - время, с. Число Фурье характеризует нестационарный режим и его, часто, называют "безразмерное время".

7. Число Эйлера:

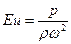
Число Эйлера характеризует соотношение сил давления и сил инерции.

В уравнения конвективного теплообмена число Е_U входит только под знаком производной, поэтому для несжимаемой жидкости существен­но не абсолютное значение давления, р , а его изменение. Вследствие этого число Эйлера обычно представляет в виде:

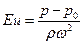или

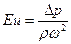
где р₀ - какое-либо фиксированное давление, например, давление на входе в канал.

Кроме названных чисел подобия существует ряд других чисел подобия, например:

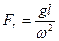- число Фруда, которое характеризует соотношение сил инерции и тяжести при вынужденном движении жидкости;

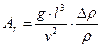- число Архимеда, определяющее условия свободного движения жидкости;

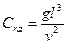- число Галилея, характеризующее соотношение сил тяжести и сил молекулярного трения.

Числа подобия F_r, A_r, G_a, G_r тождественны – это четыре различных вида одного и того же числа.

Иногда в качестве чисел подобия применяются некоторые соче­тания, образованные из приведенных выше чисел подобия. Также пре­образованные числа подобия имеют свои названия, например:

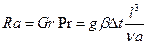- число Релея

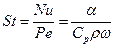- число Стантона

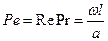- число Пекле

При расчете конвективной теплоотдачи искомыми величинами яв­ляются коэффициенты теплоотдачи α и в некоторых случаях гидрав­лическое сопротивление ∆р, которые входят соответственно в числа N_U и Е_U. В соответствии с этим числа N_U и Е_U называют опре­деляемыми числами подобия, а числа Р_r, R_е, G_r иногда и другие) - определяющими. Определяющие числа подобия называют также критериями подобия.

Согласно второй теореме подобия, уравнением подобия называют зависимость между каким-либо определяемым числом подобия и другими определяющими числами подобия. При конвективной теплоотдаче уравнения подобия могут быть представлены в следующем виде:

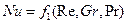
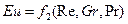
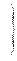(118)

Заметим, что в качестве определяемых величин в уравнениях подобия могут быть не только числа подобия, но и другие безразмерные величины, например, безразмерная температура θ, безразмерная скорость W и т.д. Т.к. нас интересует, главным образом, опре­деление коэффициента теплоотдачи, то дальше мы будем говорить об уравнениях подобия, где в качестве определяемого входит число N_U.

Уравнение (117) записано для смешанной, свободно-вынуж­денной конвекции.

Для вынужденного движения жидкости, при развитом турбулент­ном режиме, свободной конвекцией можно пренебречь. Следовательно, в этом случае из уравнения (117) выпадет число G_r.

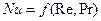(119)

При свободной конвекции в отсутствии вынужденного движения жидкости в уравнении (117) выпадает число R_е.

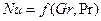(120)

По найденному из уравнения подобия значению числа N_U на­ходят коэффициент теплоотдачи:

α= N_U*λ_ж/ℓ

Опытное исследование теплоотдачи показало, что α будет иметь разные значения в условиях нагревания и охлаждения стенки.

Это явление связано с изменением физических параметров жидкости в пограничном слое. Для получения уравнений подобия, одинаково справедливых как для нагревания, так и для охлаждения, в них вводят дополнительные отношения:

t_ж/t_ст; μ_ж/μ_ст; P_rж/P_rст

где индекс "ж" означает, что данный параметр взят при темпера­туре жидкости, а индекс "ст" - при температуре стенки. Первое отношение обычно применяют при расчете теплоотдачи газов, осталь­ные - при расчете теплоотдачи капельных жидкостей.

Академик М.А.Михеев рекомендует учитывать направление теп­лового потока отношением:

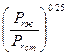
Уравнения подобия (или критериальные уравнения) обычно представляют в виде степенных функций

Тогда уравнение (117) для свободно-вынужденной конвекции принимает вид:

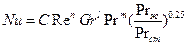(121)

Для вынужденной конвекции:

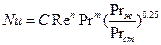(122)

Для свободной конвекции:

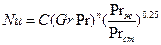(123)

Количественная связь между числами подобия, т.е. нахождение c, n, l, m и т.д. и является предметом экспериментальных исследова­ний. В качестве примера приведем уравнения подобия для некоторых конкретных случаев.

При вынужденном движении жидкости в трубах в случае ламинар­ного режима течения (R_e<2000), когда будет иметь место вязкост­но-гравитационный характер движения, т.е. будет наличие вынужден­ной и свободной конвекции (G_r*Р_r >8*10³), получено:

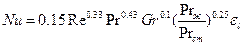
При развитом турбулентном вынужденном движении жидкости в трубах (R_e >10⁴) уравнение подобия имеет вид:

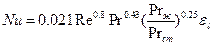
где ε_ℓ=f(ℓ/d), т.е. функция отношения длины трубы к диаметру, выбирается по специальным таблицам.

При свободном движении жидкости около горизонтальной трубы, когда будет ламинарный режим течения (10³< G_r*Р_r <10⁸), получено:

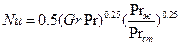
Во всех этих уравнениях вычисляется среднее значение коэффициента теплоотдачи.