Ковариация и коэффициент корреляции.

Пусть имеется двумерная случайная величина (Х иY).Степень зависимости её составляющих Х и Y, выражает ковариация и коэффициент корреляции.

Ковариацией или корреляционным моментом называется математическое ожидание произведения отклонений случайных величинХ и Y от их математического ожидания.

Обозначается:

Раскрыв скобки и преобразовав формулу,мы получим:

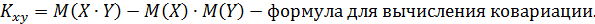
Коэффициентом корреляции называется отношение ковариации случайных величинХ и Y к произведению их средних квадратических отклонений.

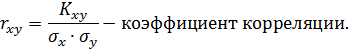
Свойства коэффициента корреляции:

1)Коэффициент корреляции принимает значение на отрезке 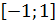, то есть

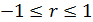
2) Если случайные величиныХ,Y независимы,то их коэффициент корреляции равен нулю, то есть .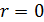

Если 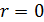, то случайные величины называются некоррелированными.

3) Если коэффициент корреляции двух случайных величин равен по модулю единице, то есть 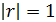,то между этими случайными величинами существует линейная функциональная зависимость.

Пример 1. Закон распределения дискретной двумерной случайной величины (X, Y) задан в таблице:

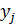
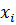
	‒1
	0,10	0,25	0,30	0,15
	0,10	0,05	0,001	0,05

Найти:

а) законы распределения одномерных случайных величин X и Y;

б) условные законы распределения случайной величины X при условии Y = 2 и случайной величины Y при условии X = 1;

в) вычислить P(Y<X);

г) ковариацию и коэффициент корреляции случайных величин X и Y.

Решение:

а) Случайная величина X может принимать значения:

X = 1 с вероятностью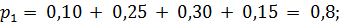

X = 2 с вероятностью 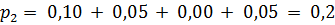, т.е. ее закон распределения:

X:

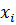
	0,8	0,2

Аналогично закон распределения:

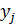
	‒1
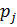
	0,2	0,3	0,3	0,2

б) Условный закон распределения X при условии, что Y = 2, получим, если вероятности 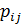, стоящие в последнем столбце первоначальной таблицы, разделим на их сумму, т.е. на . Получим:

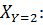
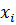
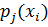
	0,75	0,25

Аналогично для получения условного закона распределения Y при условии X= 1 вероятности 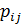, стоящие в первой строке первоначальной таблицы, делим на их сумму, т.е. на 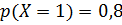. Получим:

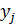
	‒1
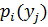
	0,125	0,3125	0,375	0,1875

в) Для нахождения вероятностей P(Y<X) складываем вероятности событий 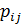из первоначальной таблицы, для которых
.

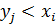Получим:

P(Y<X) = 0,10 + 0,25 + 0,10 + 0,05 + 0,00 = 0,5.

г)Найдем математические ожидания и средние квадратические отклонения этих случайных величин:

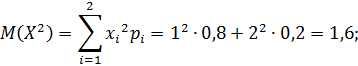
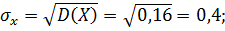
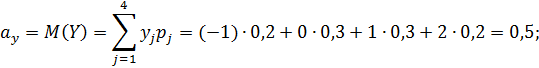
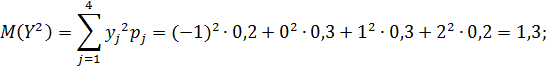
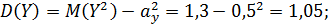
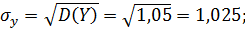
Так как

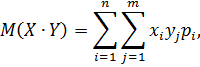
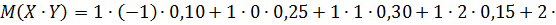
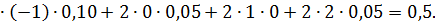
Вычислим ковариацию 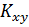по формуле:

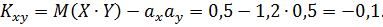
Вычислим коэффициент корреляции 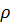по формуле:

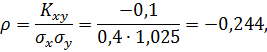
т.е. между случайными величинами X и Y существует отрицательная линейная зависимость; следовательно, при увеличении (уменьшении) одной из случайных величин другая имеет некоторую тенденцию уменьшаться (увеличиваться).