Лекция 18. ЧИСЛОВЫЕ РЯДЫ.СУММА РЯДА.

Задача суммирования множества слагаемых решается в теории рядов.

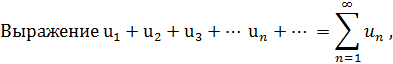
где u_1,u_2,u₃…., u_n…–члены бесконечной числовой последовательности, называется числовым рядом.

Числа u_1,u_2,u₃…., u_n… называют членами ряда, а u_n– общий член ряда.

Сумма конечного числа n первых членов ряда называется n–й частичной суммой ряда.

S_n= u₁ + u₂ +… + u_n,

т.е. S₁= u₁; S₂= u₁+ u₂

S_n= u₁+ u₂+…+ u_n

Ряд называется сходящимся, если существует конечный предел частичной суммы S_nпри n 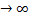, то есть

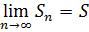
Число S называется суммой ряда.

В противном случае:

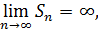
Тогда ряд называется расходящимся.

Эталонные ряды.

1. Геометрический ряд (геометрическая прогрессия)

.

.

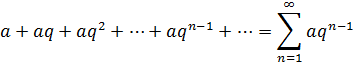
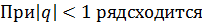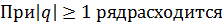Пример.

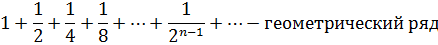
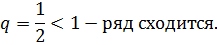
2. Гармонический ряд.

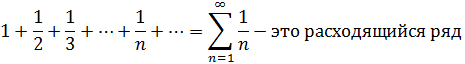
3. Обобщенный гармонический ряд.

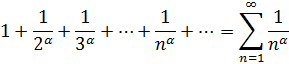
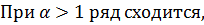
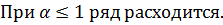
Пример.

.

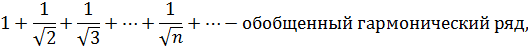
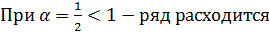Признаки сходимости знакоположительных рядов

Теорема 1. Необходимый признак сходимости.

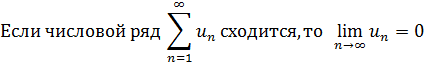
C помощью этого признака можно установить расходимость ряда.

Пример.

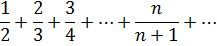
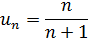
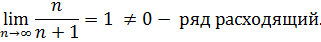
Достаточные признаки

Теорема 1.Признак сравнения рядов.

Пусть даны два знакоположительных ряда:

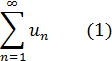
и

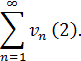
Причем 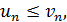тогда, если ряд (2) сходится, то сходится и ряд (1).

Если ряд (1) расходится, то расходится и ряд (2).

Пример.

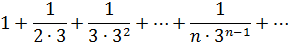
Сравним этот ряд с геометрическим рядом:

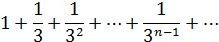
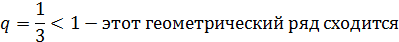
Сравним ряды:

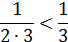
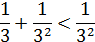
Следовательно, по признаку сравнения искомый ряд сходится.