Теорема 2. Достаточный признак сходимости знакопеременного ряда.

Если для знакопеременного ряда сходится ряд, составленный из абсолютных величин его членов 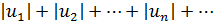, то данный знакопеременный ряд сходится.

Пример: исследовать ряд на сходимость:

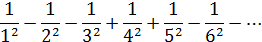
Решение:

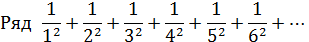
из абсолютных величин членов исходного ряда сходится, как обобщенный гармонический ряд при .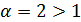

Следовательно, исходный ряд сходится.

Этот признак является достаточным, но не необходимым, то есть существуют знакопеременные ряды, которые сходятся, хотя ряды, составленные из абсолютных величин, расходятся.

Определение 1.Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.

Определение 2.Знакопеременный ряд называется условно сходящимся, если сам рядсходится, а ряд, составленный из абсолютных величин его членов, расходится.

Отличие между ними в том, что абсолютно сходящийся ряд сходится из-за того, что его члены быстро убывают, а условно сходящийся ряд сходится из-за того, что положительные и отрицательные члены уничтожают друг друга.

Пример.

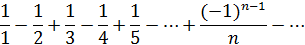
Решение:

Применим признак Лейбница:

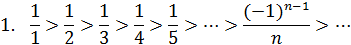
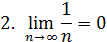
Следовательно, ряд сходится по Лейбницу. Но ряд составленный из абсолютных величин его членов расходится, как гармонический.

Значит, исходный ряд сходится условно.