Теорема 2. Признак Даламбера.
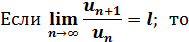
1) при 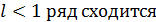
2) при 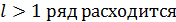
3) при 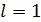 вопрос о сходимости остается открытым.
вопрос о сходимости остается открытым.
Пример.Исследовать на сходимость ряд:
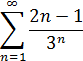
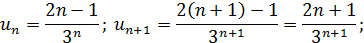
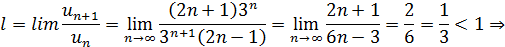
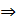 по признаку Даламберу ряд сходится.
по признаку Даламберу ряд сходится.
Теорема 3.Радикальный признак Коши.
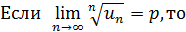
1) при 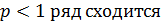
2) при 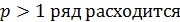
3) при 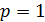 вопрос о сходимости остается открытым.
вопрос о сходимости остается открытым.
Пример:исследовать на сходимость числовой ряд:
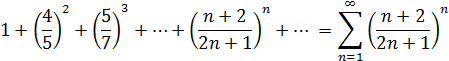
Решение:
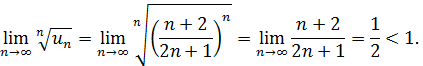
Следовательно, ряд сходится по Коши.
Теорема 4. Интегральный признак Коши.
Пусть члены ряда
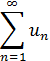
положительны и не возрастают, то есть 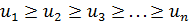 и являются значениями непрерывной невозрастающей функции f(x) при x= 1, 2, …, n.
и являются значениями непрерывной невозрастающей функции f(x) при x= 1, 2, …, n.
Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл:
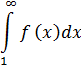
Пример.
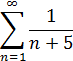
Решение:
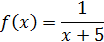
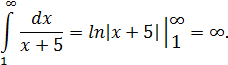
Следовательно, ряд расходится, так как расходится несобственный интеграл.
Лекция 19. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ. ПОНЯТИЕ АБСОЛЮТНОЙ И УСЛОВНОЙ СХОДИМОСТИ ЗНАКОПЕРЕМЕНОГО РЯДА.
Ряд называется знакопеременным, если любой его член может быть, как положительным, так и отрицательным.
Рассмотрим знакочередующиеся ряды:
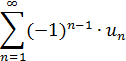
Дата добавления: 2015-12-16; просмотров: 973;
