Лекция 20. СТЕПЕННЫЕ РЯДЫ. ОБЛАСТЬ СХОДИМОСТИ. ТЕОРЕМА Н. АБЕЛЯ.
Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции.
Определение 1. Степенным рядом называется ряд вида:
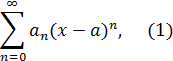
где aи коэффициенты а0,… ,аn – постоянный.
При а=0 степенной ряд примет вид:
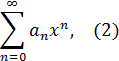
Определение 2.Совокупность значений x, при которых степенной ряд сходится, называется областью сходимостью степенного ряда.
Пример.Найти область сходимости.
1+x+ x2 + … + xn +…
Это геометрический рядq = x. Он сходится при 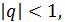 то есть при
то есть при 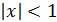 или
или 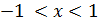 следовательно, область сходимости (−1; 1).
следовательно, область сходимости (−1; 1).
Структура области сходимости степенного ряда устанавливается с помощью теоремы Н. Абеля:
1. Если степенной ряд (2) сходится приx = x0≠ 0, то он абсолютно сходится и при всех значениях x, удовлетворяет неравенству 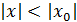 .
.
2. Если степенной ряд (2) расходится приx = x1≠ 0, то он расходится и при всех значениях x, удовлетворяет неравенству 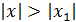 .
.
Из теоремы Н. Абеля следует, что существует такое число R ≥ 0, что при всех 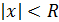 ряд (2) сходится, а при
ряд (2) сходится, а при 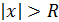 расходится.
расходится.
Число Rназывается радиусом сходимости степенного ряда, а интервал (−R; R) называется интервалом сходимости.
На концах интервала сходимости ряд (2) может, как сходится, так и расходится.
Для ряда (1) получим:
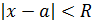 , то есть
, то есть 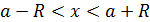 .Следовательно, интервал сходимости ряда (1) имеет вид:
.Следовательно, интервал сходимости ряда (1) имеет вид: 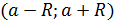 .
.
Радиус сходимости степенного ряда находится по формуле:
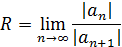
Пример 1.
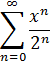
Решение:
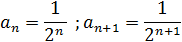
Тогда
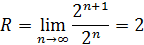
Следовательно, (−2; 2) – интервал сходимости.
При 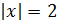 ряд расходится, так как
ряд расходится, так как
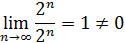
То есть
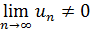
Следовательно,при 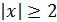 ряд расходится.
ряд расходится.
Пример 2.
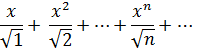
Решение:
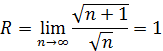
Тогда (−1;1) – интервал сходимости.
При x=1ряд расходится, как обобщенный гармонический.
При x=−1 получим знакочередующийся ряд.
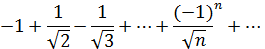
На основании признака Лейбница он сходится, т.к.
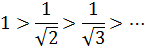
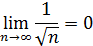
Следовательно, область сходимости −1≤x˂1
Свойства степенных рядов
Пусть степенной ряд
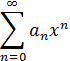
имеет интервал сходимости 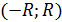 .
.
Тогдаряд, полученный из данного ряда почленным дифференцированием или интегрированием, имеет тот же интервал сходимости.
Следовательно, на интервале сходимости степенные ряды можно почленно дифференцировать и интегрировать.
Дата добавления: 2015-12-16; просмотров: 1144;
