Дискретизация и восстановление сигналов
Под дискретизацией сигналов (в узком смысле) понимают преобразование аналогового сигнала x(t) в последовательность отсчётов его мгновенных значений, взятых через интервалы времени Dt (рис. 2.5)
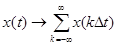 , k = 0, ±1, ±2,…,
, k = 0, ±1, ±2,…,
Dt – шаг дискретизации,
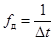 – частота дискретизации.
– частота дискретизации.
 x(t)
а
t
xд(t)
б
t
yр(t)
1 в
t
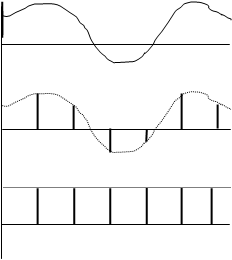
Рис. 2.5. Дискретизация сигнала x(t)
а
t
xд(t)
б
t
yр(t)
1 в
t
Рис. 2.5. Дискретизация сигнала
|
Для аналитического описания процесса дис-кретизации используем решётчатую функцию 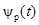 (рис. 2.5, в) вида
(рис. 2.5, в) вида 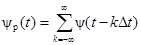 ,
,
где 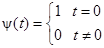 .
.
Функция 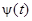 связана с функцией 1(t) (единичного скачка) и d-функцией следующим образом
связана с функцией 1(t) (единичного скачка) и d-функцией следующим образом
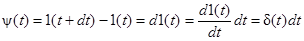 . (2.8)
. (2.8)
Введение функции 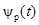 позволяет процесс дискретизации аналогового сигнала x(t) выразить произведением вида (рис. 2.5, б)
позволяет процесс дискретизации аналогового сигнала x(t) выразить произведением вида (рис. 2.5, б)
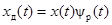 .
.
Как и d-функция 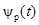 обладает фильтрующим свойством
обладает фильтрующим свойством
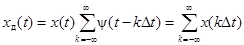 .
.
Поскольку 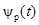 периодическая функция с периодом Dt, то её можно представить рядом Фурье
периодическая функция с периодом Dt, то её можно представить рядом Фурье
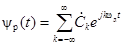 , где
, где
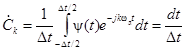 (фильтрующее свойство!)
(фильтрующее свойство!)
и, следовательно, 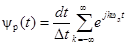 .
.
Учитывая свойство спектральной функции комплексного гармонического колебания (2.6) и выражение (2.8), имеем
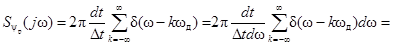
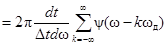 .
.
Исходя из очевидных соотношений 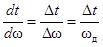 , получим
, получим
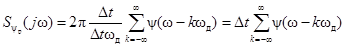 . (2.9)
. (2.9)
Окончательно
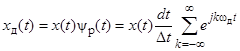 (2.10)
(2.10)
и по свойству смещения спектра (2.7)
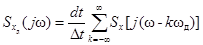 .
.
Из (2.10) вытекает, что процесс дискретизации сигналов можно реализовать на перемножителе (рис.2.6).





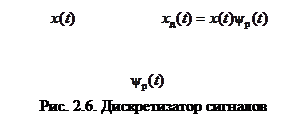 |
Дискретизация сигналов широко используется в системах связи. Она является необходимой операцией при передаче аналоговых сигналов по цифровым каналам (для преобразования аналогового сигнала в цифровой поток его отсчётов) и в системах многоканальной передачи с временным уплотнением (для разделения заданного множества аналоговых сигналов во временной области). Во всех этих случаях важнейшими являются вопросы о выборе частоты дискретизации сигналов, способе их восстановления (обратного преобразования отсчётов в аналоговый сигнал) и степени искажений в процессе таких преобразований. Ответы на эти вопросы даёт теорема отсчётов (часто называемая именем Котельникова В.А. – автора одного из её доказательств в 1933 г.).
Теорема отсчётов
Любой F-финитный сигнал (сигнал с ограниченным частотой Fв спектром) точно определяется последовательностью своих отсчётов, взятых через интервалы 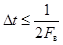 .
.
Справедливость этого утверждения следует из рассмотрения спектров, приведённых на рис. 2.7. На рис. 2.7(а) изображён двусторонний спектр исходного аналогового сигнала 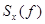 , ограниченный частотой
, ограниченный частотой 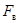 . На рис. 2.7(б) –спектр решетчатой функции
. На рис. 2.7(б) –спектр решетчатой функции 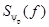 , построенный по выражению (2.9). На рис. 2.7 (в, г и д) представлены спектры дискретизированного сигнала
, построенный по выражению (2.9). На рис. 2.7 (в, г и д) представлены спектры дискретизированного сигнала 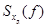 при разных соотношениях частот дискретизации
при разных соотношениях частот дискретизации 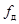 и
и 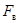 . Обратите внимание, что в результате дискретизации сигнала его спектр периодически повторяется по оси частот с периодом
. Обратите внимание, что в результате дискретизации сигнала его спектр периодически повторяется по оси частот с периодом 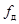 .
.
Исходя из свойства взаимно однозначного соответствия 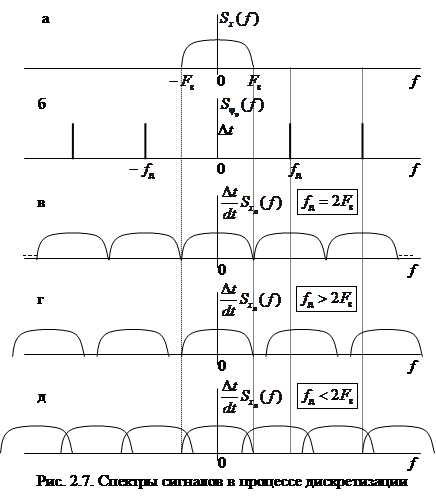 временного и спектрального представлений сигнала, можно утверждать, что точное восстановление сигнала в аналоговой форме по его отсчётам возможно, если из спектров
временного и спектрального представлений сигнала, можно утверждать, что точное восстановление сигнала в аналоговой форме по его отсчётам возможно, если из спектров 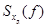 (рис.2.7 (в, г и д)) можно получить спектр
(рис.2.7 (в, г и д)) можно получить спектр 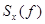 (рис. 2.7 (а)). Очевидно, что это достижимо:
(рис. 2.7 (а)). Очевидно, что это достижимо:
1) фильтрацией дискретизированного сигнала с помощью идеального ФНЧ с частотой верхнего среза 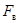 ,
,
2) только в случае 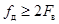 , когда отсутствует наложение спектров, такое, как показано на рис. 2.7 (д).
, когда отсутствует наложение спектров, такое, как показано на рис. 2.7 (д).
Таким образом, процедура восстановления сигнала по 
отсчётам может быть осуществлена идеальным ФНЧ с передаточной функцией
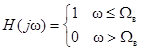 ,
, 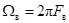
и, соответственно, с импульсной характеристикой
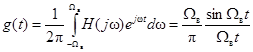 .
.
Поскольку импульсная характеристика цепи есть её реакция на воздействие в виде d-функции 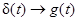 , то легко определить реакцию идеального ФНЧ на дискретизированный сигнал
, то легко определить реакцию идеального ФНЧ на дискретизированный сигнал 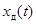
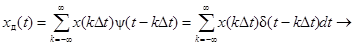
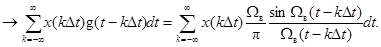 Выражение
Выражение 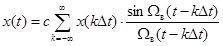 известно в литературе как ряд Котельникова (с масштабным коэффициентом с) и представляет собой частный случай обобщенного ряда Фурье, где базисом является система функций
известно в литературе как ряд Котельникова (с масштабным коэффициентом с) и представляет собой частный случай обобщенного ряда Фурье, где базисом является система функций 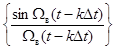 , а коэффициентами разложения служат отсчёты мгновенных значений сигнала
, а коэффициентами разложения служат отсчёты мгновенных значений сигнала 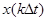 .
.
На практике абсолютно точное восстановление сигналов по их отсчётам невозможно по следующим причинам:
1) Идеальный ФНЧ–физически нереализуемая цепь, т.к. его импульсная характеристика отлична от 0 при t<0. Характеристики реальных ФНЧ могут быть приближены к идеальным лишь с определенной погрешностью, тем меньшей, чем больше задержка.
2) Реальные сигналы являются Т-финитными, а следовательно имеют неограниченный по частоте спектр. Если всё же спектр сигнала ограничить частотой 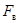 , то на интервале существования сигнала Т число независимых отсчётов N, определяющих сигнал с заданной погрешностью, становится конечным
, то на интервале существования сигнала Т число независимых отсчётов N, определяющих сигнал с заданной погрешностью, становится конечным
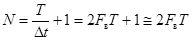 ,
,
где 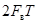 – база сигнала.
– база сигнала.
При осуществлении дискретизации сигнала, когда частота дискретизации 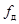 выбрана, необходимо использовать антиэлайсинговыйФНЧ с частотой верхнего среза
выбрана, необходимо использовать антиэлайсинговыйФНЧ с частотой верхнего среза 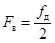 для ограничения спектра сигнала и предотвращения тем самым искажений, вызванных перекрытием спектров (рис.2.4 (д)) (антиэлайсинговый – от слова «элайсинг», означающего наложение спектров).
для ограничения спектра сигнала и предотвращения тем самым искажений, вызванных перекрытием спектров (рис.2.4 (д)) (антиэлайсинговый – от слова «элайсинг», означающего наложение спектров).
Контрольные вопросы
1. В чём заключается операция дискретизации непрерывных сигналов? Как её записать математически?
2. Как изменяется спектр сигнала в результате его дискретизации?
3. Приведите примеры практического использования дискретизации сигналов в системах связи.
4. Сформулируйте теорему отсчётов. В чём состоит её фундаментальное значение?
5. Из каких соображений выбирается частота дискретизации непрерывных сигналов?
6. Каким образом и каким ФУ обеспечивается восстановление непрерывного сигнала по его отсчётам?
7. Укажите причины погрешностей восстановления непрерывных сигналов по их отсчётам.
8. Напишите выражение сигнала в виде ряда Котельникова.
9. Какой базис используется при разложении сигналов в ряд Котельникова?
10. Как определяются коэффициенты разложения сигналов в ряд Котельникова?
11. Объясните необходимость использования антиэлайсингового фильтра при дискретизации сигналов.
12. Приведите примеры проявления искажений, связанных с наложением спектров сигнала после его дискретизации (при 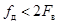 ).
).
Дата добавления: 2016-01-03; просмотров: 5922;
