Понятие точечной оценки параметров сигнала

Как известно сигнал поступающий на приемную сторону РТС, несет существенную для получателя информацию, содержащуюся в значениях тех или иных параметров: амплитуды, частоты, фазы, времени запаздывания и др.

Очевидно, пользователю для извлечения из полученного сигнала сведений следует определить значения параметров сигнала, несущих требуемую информацию. Устройство, предназначенное для измерения параметров сигнала, будем называть измерителем. Измеренные значения параметров не обязательно воспроизведут истинные значения параметров, так как в реальных условиях полезный сигнал поступает на приемную сторону только в смеси с помехами. Кроме того, на измерения может существенно влиять наличие у сигнала не только полезных (несущих необходимую информацию) параметров, но и параметров, не известных потребителю и не содержащих интересных для него сведений. Полезные параметры сигнала, содержащие нужную абоненту информацию, будем называть информационными, а остальные неизвестные параметры - мешающими (неинформационными, несущественными, паразитными, нежелательными).

Если в процессе измерения информационных параметров на интервале времени [0,T] их значения не изменяются, то в этом случае задача измерения параметров сводится к задаче оценки параметров сигнала. В случае же, когда зависимость информационных параметров l(t) пренебречь нельзя и требуется отслеживание меняющихся информационных параметров, такую процедуру измерения называют фильтрацией параметров сигнала. Задачу фильтрации мы рассмотрим с Вами на следующей лекции.

Пусть случайная величина 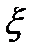имеет определенное распределение, но в нем неизвестен какой-либо параметр 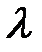. Известна условная плотность вероят­ности

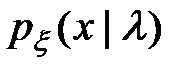. (10.1)

Для оценки неизвестного параметра 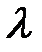, проводят наб­людения случайной величины 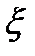и получают выборку объёма n, которую можно представить в виде n-мерного вектора

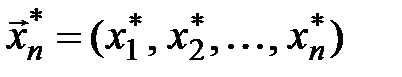, (10.2)

где результаты наблюдения являются проекциями этого вектора в n-мерном пространстве. Затем подбирают такую функцию от выборки (называемую статистикой), которую можно было бы принять за оценку параметра .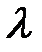

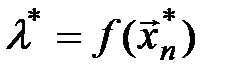. (10.3)

При конкретной выборке 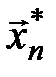эта оценка является конкретной точкой на оси оцениваемого параметра. Поэтому оценка, определяемая формулой (10.3), называется точечной.Если 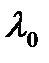истинное значение параметра, то 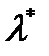будет находиться где-то вблизи точки 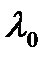(рисунок).

Для другой выборки 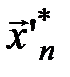точечная оценка будет находиться в другой точке оси .

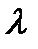Если оценка параметра получена как функция случайной выборки

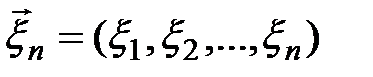. (10.4)

В этом случае оценка 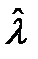является случайной величиной

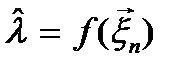. (10.5)

Оценка 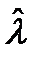имеет практическую ценность, если она обладает свойствами несмещённости, состоятельности и эффективности.

1. Несмещенной называется оценка, у которой математическое ожидание совпадает с истинным значением оценивае­мого параметра :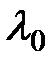

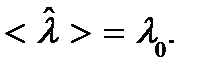
2. Состоятельной называется оценка, которая с увеличением объёма выборки n сходится по вероятности к истинному значению оцениваемого параметра:

,

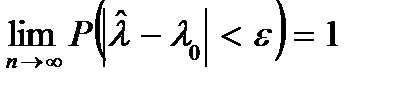где 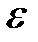- наперед заданное малое положительное число.

3. Эффективной называется оценка, которая среди любых других оценок, отличающихся видом функционального преобра­зования, но полученных для одного и того же объёма выборки, имеет наименьшую дисперсию

.

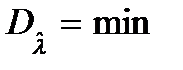На практике оценки могут иметь свойства, в той или иной сте­пени отличные от рассмотренных. При этом, чем меньше у оценки наблюдается отклонений от свойств несмещённости, состоятельности и эффективности, тем она предпочтительнее.