Различение двух детерминированных сигналов на фоне белого шума. Структурные схемы оптимальных различителей
Правило принятия решения (9.5) можно конкретизировать, если положить, что n(t) в (9.1) является гауссовским белым шумом. Для белого шума функционалы плотности вероятности будут равны:
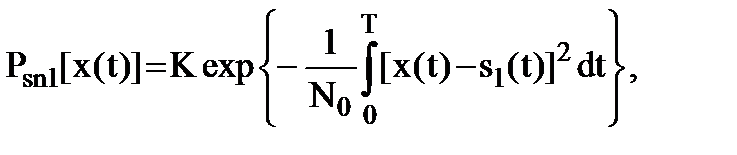 (9.6)
(9.6)
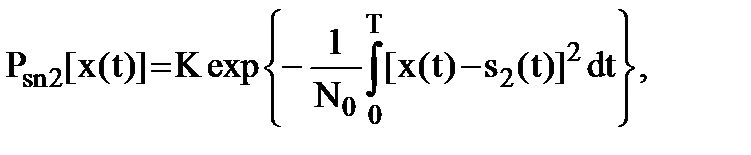 (9.7)
(9.7)
где К - коэффициент нормировки.
Если подставить (9.6) и (9.7) в (9.5), то получим
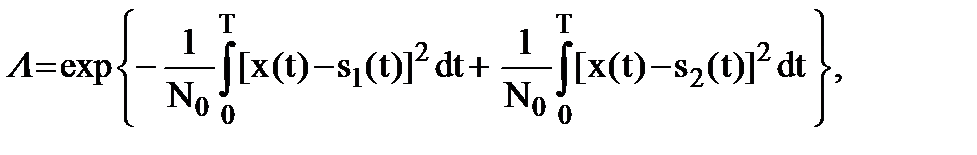
откуда
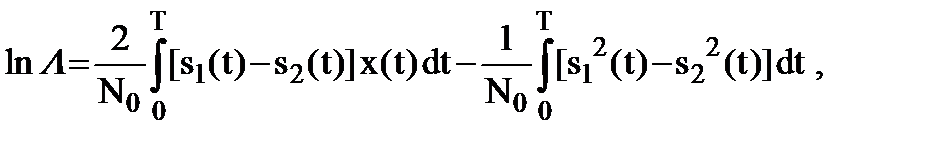
Учитывая, что
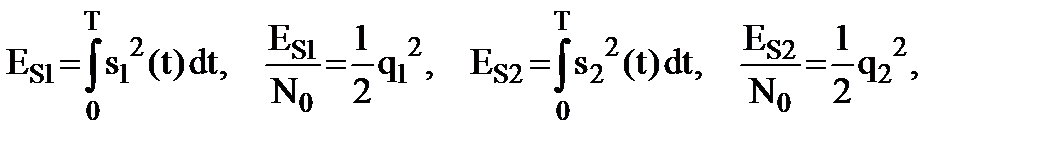
правило решения (9.5) можно записать в следующем виде
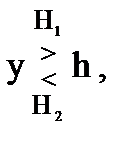 (9.8)
(9.8)
где
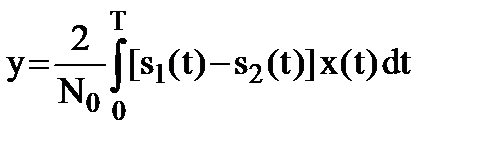 (9.9)
(9.9)
- достаточная статистика при различении детерминированных сигналов;
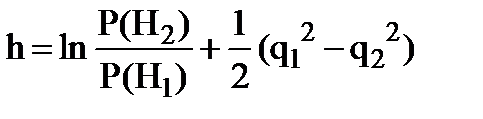 (9.10)
(9.10)
- порог для критерия идеального наблюдателя, зависящий как от априорных вероятностей Р(Н1) и Р(Н2), так и от отношений сигнал/шум по каждому сигналу.
Таким образом, в качестве достаточной статистики y в задаче различения используется разность между двумя корреляционными интегралами.
Если сигналы s1(t) и s2(t) имеют одинаковые энергии, то порог 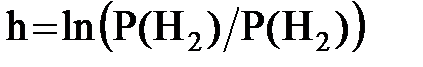 . Если к тому же вероятности гипотез Р(Н1) = Р(Н2) = 0,5, то h = 0.
. Если к тому же вероятности гипотез Р(Н1) = Р(Н2) = 0,5, то h = 0.
Возможны различные варианты реализации оптимального алгоритма различения двух детерминированных сигналов: с использованием корреляционных приемников (рис.9.1) и на основе согласованных фильтров (рис.9.2). При построении схем, приведенных на рисунках, достаточная статистика y (9.9) представлялась в виде разности интегралов
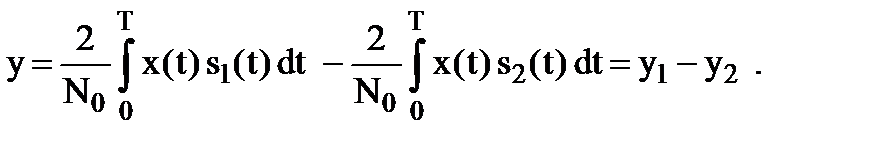
Разность величин y1 и y2 на выходах интеграторов сравнивается с порогом h. Импульсные характеристики согласованных фильтров (СФ1 и СФ2) на рис. 9.2 определяются соотношением
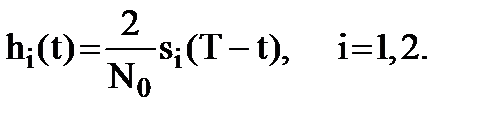

Рис. 9.1

Рис. 9.2
Возможна реализация различителя на основе одноканальной схемы. В этом случае генератор опорного сигнала (ГОС) формирует разностный сигнал (s1(t) - s2(t)), а СФ имеет импульсную характеристику 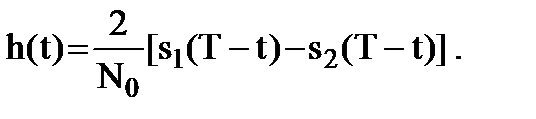 Схемы различителей одноканального типа приведены на рис.9.3 и 9.4.
Схемы различителей одноканального типа приведены на рис.9.3 и 9.4.

Рис. 9.3

Рис. 9.4
Дата добавления: 2016-01-26; просмотров: 1659;
