На фоне белого шума

Начальная фаза радиосигнала, как правило, неизвестна. В этом случае можно использовать модель сигнала

s(t,j) = V(t)cos[w₀t + y(t) ­‑ j], (8.7)

где законы амплитудной V(t) и фазовой y (t) модуляции и частота w₀ известны, а начальная фаза j неизвестна. Выражение (8.7) удобно представить в виде

s(t,j) = s₁(t)cos j + s₂(t)sin j, (8.8)

где s₁(t) = V(t)cos(w₀t + y(t)), s₂(t) = V(t)sin(w₀t + y(t)) - квадратурные составляющие сигнала.

Полагаем, что начальная фаза j является случайной величиной, при этом при отсутствии информации об априорном распределении j естественно считать это распределение равномерным

p(j) = 1/2p, - p £ j £ p. (8.9)

Такая модель радиосигнала используется в радиолокации при описании отраженных сигналов от неподвижной цели.

Отношение правдоподобия в рассматриваемой задаче обнаружения сигнала со случайной начальной фазой получается путем усреднения условного отношения правдоподобия L(x/j) по всем возможным значениям фазы

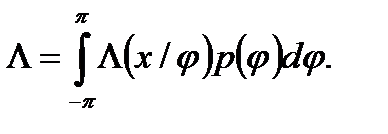(8.10)

Что касается условного отношения правдоподобия L(x/j), то оно, очевидно, совпадает с отношением правдоподобия для детерминированного сигнала s(t,j), где j - фиксированная величина. Поэтому согласно (7.17) имеем:

.

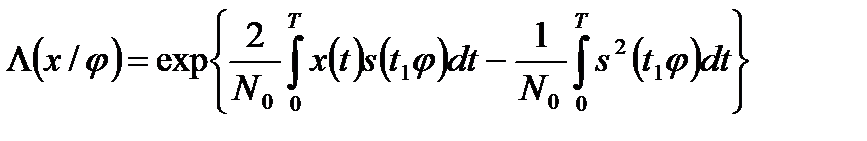Подставив в это выражение (8.8), рассмотрим получающиеся интегралы. Корреляционный интеграл

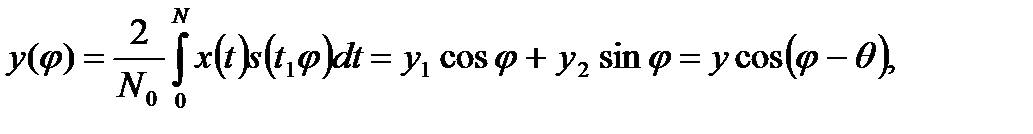
где

- его квадратурные составляющие, а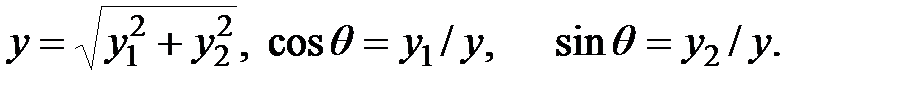

Далее, при Т >> 2p/w₀ энергия сигнала от значения фазы j практически не зависит и поэтому

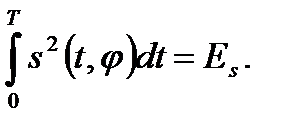
Таким образом,

.

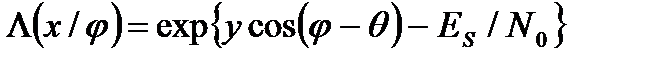Подставляя это выражение и (8.9) в (8.10), после интегрирования получаем отношение правдоподобия

(8.11)

где I₀(y) - модифицированная функция Бесселя нулевого порядка. Учитывая, что lnI₀ (y) является монотонной функцией, приходим к оптимальному алгоритму обнаружения вида

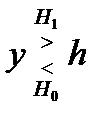, (8.12)

где

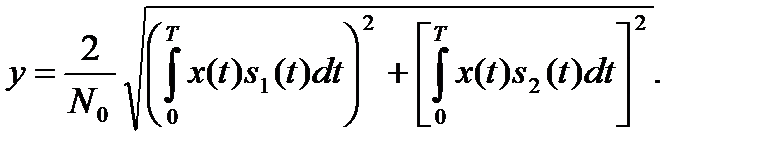(8.13)

Структурная схема обнаружителя на рис. 8.2 построена в соответствии с формулами (8.12) и (8.13). Такую схему называют квадратурным приемником. Квадратурные каналы организуют путем включения фазовращателя в цепь опорного сигнала одного из перемножителей. Квадраторы (Кв), сумматор (å), вычислитель квадратного корня ( 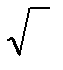) обеспечивают формирование на входе ПУ в момент времени t = T значения 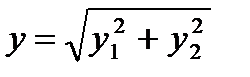. Наличие двух каналов исключает возможность потери полезного сигнала вследствие незнания его начальной фазы.

Схема обнаружителя, представленная на рис.8.2, как и схема, изображенная на рис.8.3, требует знания временного положения ожидаемого сигнала. Если время запаздывания сигнала неизвестно, схема оптимального обнаружителя усложняется. При разбиении интервала неопределенности времени запаздывания на элементарные участки, длительность каждого из которых, определяется требуемой разрешающей способностью по дальности, можно построить многоканальный корреляционный обнаружитель. Каждый канал его настраивается на сигнал с соответствующим запаздыванием. Решение об обнаружении сигнала принимается одновременно с оценкой времени запаздывания.

Рис.8.2

В радиолокации особо распространенным является прием сигналов с произвольным временем запаздывания. Поэтому в целях упрощения конструкции обнаружителя удобнее использовать фильтровой вариант его построения (рис.8.3), позволяющего обеспечить оптимальное обнаружение сигналов с произвольным временем запаздывания при наличии всего лишь одного приемного канала. Возможность использования согласованных фильтров в обнаружителях сигналов со случайной фазой основывается на следующих рассуждениях. Величина достаточной статистики y, которую должен формировать обнаружитель, есть огибающая колебания y×cos(j - q), иначе говоря, огибающая корреляционного интеграла у(j). Это колебание, можно сформировать пропустив наблюдаемый процесс x(t) через фильтр, согласованный с сигналом s(t, j), то есть имеющий импульсную характеристику вида h(t) = 2/N₀ s(T - t, j) (здесь j - фиксированная величина). Отметим, что поскольку результат обработки у не зависит от значения начальной фазы j, то ее при реализации фильтра можно брать любой, в частности можно положить j = 0. Огибающая y(t) на выходе согласованного фильтра, на вход которого поступает процесс s(t) + n(t), выделяется амплитудным детектором (АД), при этом результат детектирования в момент времени t = T должен подаваться на пороговое устройство (см. рис.8.3).

Перейдем к расчету показателей качества обнаружения. Так как огибающая y(t) шума и смеси сигнала с шумом на выходе СФ распределена по закону Релея и обобщенному закону Релея (закону Райса) соответственно, то вероятности ложной тревоги и правильного обнаружения для обнаружителя, работающего по алгоритму (8.12), равны:

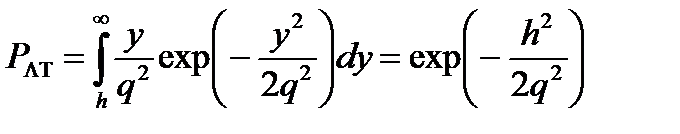, (8.14)

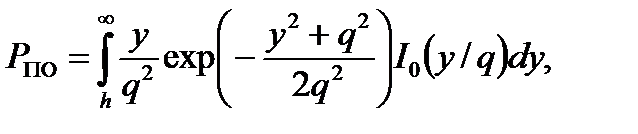(8.15)

где .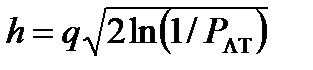

Характеристики обнаружения сигнала со случайной начальной фазой (штрихованные линии на рис.8.1) построены в соответствии с (8.14) и (8.15). По сравнению с характеристиками обнаружения детерминированного сигнала они сдвинуты вправо, то есть для обнаружения сигнала со случайной начальной фазой требуется несколько большее пороговое отношение сигнал/ шум.

Рис.8.3