Двухмерная адаптивная фильтрация.

Прежде чем перейти к построению двумерного адаптивного фильтра, приведем обобщенную схему обычной двумерной линейной оптимальной фильтрации геофизических полей, которая заключается в следующем:

-рассчитывается двумерная автокорреляционная функция 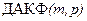по всей площади наблюдения, здесь 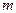-величина смещения по пикетам, 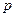-величина смещения между профилями.

-по значениям радиусов корреляции между пикетами 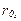и профилями 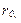выбирается соответственно ширина 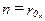(число пикетов) и высота 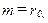(количество профилей) окна фильтрации.

-по форме 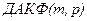определяется наклон окна фильтрации 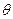, который, как правило, совпадает с направлением простирания наиболее энергоемких аномалий.

-в зависимости от критерия оптимальности, на основе имеющейся информации о спектрально-корреляционных свойствах полезного сигнала и помех, или на основе их оценок, вычисляются весовые коэффициенты двумерного фильтра .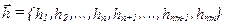

-в скользящем окне фиксированных размеров и выбранного наклона осуществляется двумерная свертка исходного поля с весовыми коэффициентами фильтра.

Таким образом, основные параметры двумерного фильтра (весовые коэффициенты 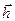, ширина 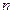, высота 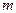и наклон окна 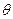фильтрации) определяются один раз для всей площади наблюдений.

Как и в случае одномерной фильтрации необходимые для расчета весовых коэффициентов фильтра оценки корреляционных характеристик полезного сигнала и помех, при не выполнении условия стационарности поля, не являются состоятельными. Так, структура двумерной автокорреляционной функции 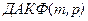, рассчитанной по всем точкам площади наблюдений, отражает корреляционные характеристики наиболее энергоемких аномалий, что не позволяет осуществить фильтрацию с целью оценки параметров менее энергоемких и имеющих отличное от основного простирание аномалий.

Алгоритм построения двумерного адаптивного энергетического фильтра, предназначенного для обработки нестационарных геофизических полей, настраивающегося на изменение спектрально-корреляционных характеристик аномалии и помех по площади, непосредственно в процессе фильтрации заключается в следующем:

1.Как и при обычной двумерной фильтрации, по всей площади наблюдений для определения корреляционных характеристик и размеров наиболее энергоемких (чаще всего и протяженных) аномалий рассчитывается двумерная автокорреляционная функция .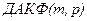

2.По значениям радиуса корреляции 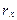вдоль профилей и между ними 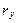выбираются размеры так называемого двумерного базового окна[8] двумерного адаптивного фильтра (соответственно ширина 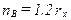в пикетах и высота 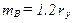в профилях), которые при таком подходе заведомо больше размеров самых энергоемких аномалий.

3.Базовое окно размещается в левом верхнем углу исследуемой площади и по значениям поля, попадающим в окно, рассчитывается текущая двумерная автокорреляционная функция .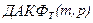

4.По 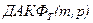определяются текущие значения радиусов корреляции между пикетам 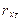и профилям 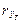, а также значения ширины 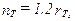, высоты 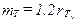и наклона 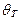текущего окна фильтрации.

5.Из уравнения 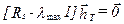находятся весовые коэффициенты фильтра 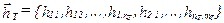( 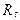-оценка расширенной корреляционной матрицы полезного сигнала размерностью 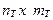, 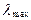-максимальное собственное значение матрицы ).

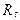6.Осуществляется двумерная свертка значений поля 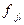с весовыми коэффициентами фильтра

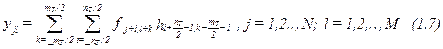
и результат относится к центральной точке базового окна.

7.Базовое окно смещается по пикетам и профилям и процедура повторяется, начиная с третьего шага схемы.

Таким образом, при адаптивной фильтрации, в окрестностях базового окна каждой точки наблюдения, осуществляется локальная фильтрация с уникальными параметрами и весовыми коэффициентами фильтра, отражающими изменение спектрально ‑ корреляционных характеристик поля по площади. Так, если в окрестностях определенной точки отсутствуют аномалии, то ширина и высота окна фильтрации будут минимальными. При наличии в окрестностях точки самых энергоемких и протяженных аномалий ширина и высота окна фильтрации будут максимальными, но не превышающими размеров базового окна.

Как и в одномерном случае, важнейшие параметры предложенного выше алгоритма двумерного адаптивного фильтра: размеры базового окна 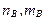, ширина 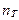и высота 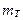текущего окна фильтрации, связаны с переменными 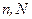и и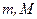з выражения для операции дискретной двумерной свертки.

Для иллюстрации преимущества предлагаемого алгоритма рассмотрим результаты, полученные при обработке модельного поля (рис. 6.3.a) неадаптивным и адаптивным двумерным энергетическим фильтром. Модельное поле представлено суммой некоррелированной помехи и 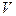-образной положительной аномалии при этом ее амплитуда соизмерима с дисперсией помехи.

На рисунках 6.3.b и 6.3.c изображены результаты фильтрации исходных данных неадаптивным двумерным энергетическим фильтром соответственно при северо-восточном и северо-западном наклонах окна фильтрации. В первом случае наклон окна совпадает с простиранием правой ветви аномалии, во втором - с простиранием левой ветви. Результаты фильтрации адаптивным двумерным энергетическим фильтром приведен на рисунке 6.3.d.

Анализируя полученные результаты, можно сделать вывод о том, что использование обычного (неадаптивного) фильтра приводит к "размыванию" аномалии при несовпадении наклона окна фильтрации с простиранием аномалии. Так, при северо-западном наклоне окна искажается форма левой ветви аномалии, а при северо-восточном наклоне окна - правой. Применение адаптивного фильтра позволяет избежать подобного отрицательного эффекта за счет его способности адаптироваться к изменению корреляционных характеристик поля непосредственно в процессе фильтрации.

Рис.6.3.a. Исходное модельное поле.	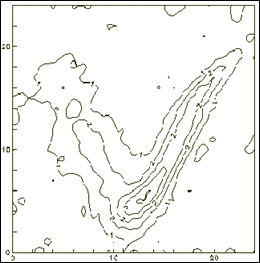Рис. 6.3.b. Северо-восточный наклон окна фильтрации.
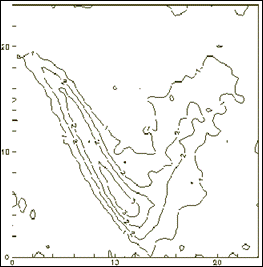Рис.6.3.с. Северо-западный наклон окна фильтрации.	Рис.6.3.d. Результат двумерной адаптивной фильтрации.

Очевидно, что, как и в одномерном случае, в рамках предложенного подхода, не представляет трудностей реализация различных оптимальных (винеровского, согласованного) и неоптимальных двумерных адаптивных фильтров. В программном комплексе "КОСКАД3Dt" реализованы энергетический, энтропийный, медианный и другие.