Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ)

Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака 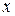, на результативный признак 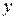и представляющая собой однофакторный корреляционный и регрессионный анализ.

При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи ( уравнение регрессии)имеет вид:

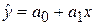, (9.3)

где 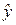- теоретические значения результативного признака, полученные по уравнению регрессии;

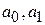- коэффициенты (параметры) уравнения регрессии.

Поскольку 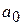является средним значением 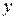в точке 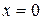, экономическая интерпретация часто затруднена или вообще невозможна.

Коэффициент парной линейной регрессии 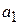имеет смысл показателя силы связимежду вариацией факторного признака 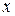и вариацией результативного признака 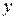.Уравнение (9.3) показывает среднее значение изменения результативного признака 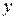при изменении факторного признака 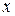на одну единицу его измерения, т.е. вариацию 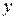, приходящуюся на единицу вариации 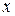. Знак 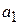указывает направление этого изменения.

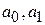
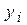Параметры уравнения находят методом наименьших квадратов- метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений. Таким образом, в основу данного метода положено требование минимальности сумм квадратов отклонений эмпирических данных от выровненных :

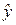Для нахождения минимума функции приравниваем к нулю её частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

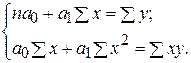(9.4)

Решим эту систему в общем виде, находим параметры уравнения :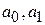

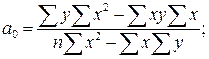(9.5)

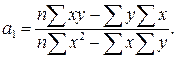(9.6)

Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:

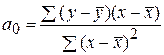или ,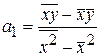

.

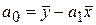Определив значения 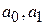, подставив их в уравнение связи 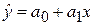, находим значения 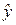, зависящие только от заданного значения .

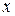Пример 9.1.Рассмотрим построение однофакторного уравнения регрессии зависимости объема предоставленных кредитов 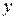от задолженности по кредитам .

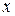Исходя из экономических соображений предоставленные кредиты выбраны в качестве независимой переменной 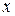. Сопоставление данных параллельных рядов признаков 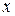и 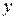(таблица 9.1) показывает, что с возрастанием признака 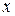(предоставленные в рублях кредиты), растет результативный признак 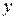(задолженность по кредитам в рублях). Следовательно, между 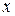и 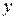существует прямая зависимость, выраженная достаточно ясно.

Таблица 9.1 - Распределение лет по сумме предоставленных кредитов и задолженности по ним, в рублях

Исходные данные	Расчетные данные
Год	Предоставленные кредиты в рублях, млрд. руб.	Задолженность по кредитам в рублях, млрд. руб.
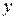
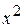
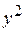
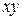
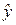
	1,935 3,048 4,244 6,538 10,183	1,539 2,306 3,079 4,375 6,738	3,744 9,290 18,012 42,745 103,693	2,369 5,318 9,480 19,141 45,401	2,978 7,029 13,067 28,604 68,613	1,661 2,329 3,046 4,423 6,610
Итого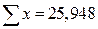

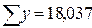
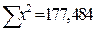
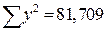
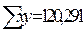
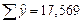
Пользуясь расчетными значениями (см. таблицу 9.1), исчислим параметры для данного уравнения регрессии:

,

.

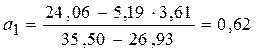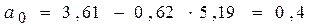Следовательно, регрессионная модель распределения задолженности по предоставленным кредитам в рублях дляданного примера может быть записана в виде конкретного простого уравнения регрессии:

.

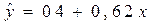Это уравнение характеризует зависимость среднего уровня предоставленных в рублях кредитов от задолженности по ним. Расчетные значения 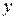, найденные по данному уравнению, приведены в таблице 9.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм 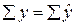( 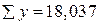,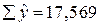(возникло некоторое расхождение вследствие округления расчетов)).

Корреляционный анализ имеет своей задачей количественное определение тесноты связи не только между двумя признаками (при парной связи), но и между результативным признаком и множеством факторных признаков (при многофакторной связи).