Фильтр Колмогорова-Винера и его применение.

Фильтр Колмогорова-Винера строится на основе критерия минимума среднеквадратического отклонения 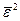профильтрованного сигнала 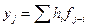от желаемого сигнала 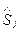на выходе фильтра, т.е.

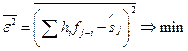(7.1.).

Черта сверху означает усреднение ошибки отклонения 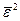по всем j-ым значениям. Впервые критерий был сформулирован А.Н.Колмогоровым в 1939 г. И им было выведено на его основе уравнение фильтра для решения задачи сглаживания. Н.Винер в 1949 г. повторил результат А.Н.Колмогорова, но Н.Винер был первым, кто реализовал практическое применение уравнения для решения ряда технических задач. В зарубежных публикациях этот фильтр известен как винеровский фильтр (Wiener filter).

А.Н.Колмогоров сформулировал критерий в предположении о стационарном случайном характере сигнала и помех с известными их корреляционными свойствами, т.е. с известными АКФ, или их спектральными свойствами, т.е. с известными энергетическими спектрами.

В этих предположениях минимизация среднеквадратической ошибки отклонения профилированного сигнала от желаемого для выражения (7.1) приводит к решению системы линейных уравнений вида:

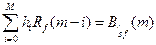(7.2)

Уравнение (7.2) представляет дискретный аналог уравнения Колмогорова-Винера, которое для непрерывных стационарных процессов выражается как 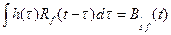и известно под названием уравнения Винера-Хопфа.

В выражении (7.2) h_i – искомая весовая функция фильтра; 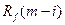- корреляционная матрица исходных данных; 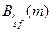- взаимно корреляционная функция желаемого сигнала 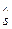с исходными данными f.

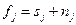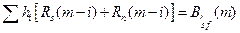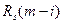При аддитивной модели поля выражение (7.2) можно переписать как: , где и 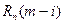- корреляционные матрицы сигнала и помех, построенные при заданных АКФ.

Правую часть (7.2) с учетом независимости сигнала и помехи можно записать в виде .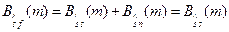

Если принять, что желаемый сигнал 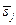на выходе фильтра совпадает с исходным сигналом на входе 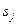, т.е. 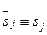, то 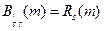и система уравнений (7.2) преобразуется в следующую систему:

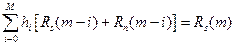(7.3)

где 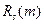- АКФ сигнала .

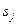Из уравнения (7.3) следует, что при заданных АКФ сигнала и помех можно найти искомую весовую функцию h_i. Фильтр (7.3) получил название фильтра воспроизведения сигнала. С учетом четности автокорреляционных функций в (7.3) используются значения АКФ лишь для положительных значений m.

Выражение (7.3) можно представить в матричной форме 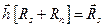или 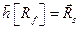(7.4) , где 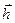и 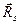- матрица-строка соответственно для весовой функции и АКФ сигнала. 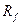- корреляционная матрица исходного поля, т.е.

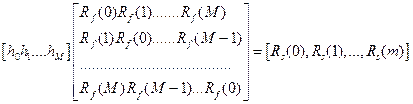(7.4)

Из последней системы уравнений при заданной АКФ сигнала 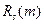и АКФ наблюденного поля 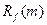находятся (М+1) – значения весовой функции. Для реализации процедуры сглаживания при воспроизведении сигнала необходимо осуществить свертку исходных данных 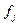с найденной весовой функцией , т.е. .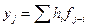

Пример 1. Пусть сигнал на входе фильтра представлен двумя значениями S₀=3 и S₁=1, а некоррелированная помеха с единичной дисперсией n₀=1; n₁=0. Тогда АКФ сигнала без учета его осреднения состоит из двух значений: 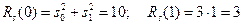, АКФ помехи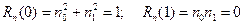

Уравнение Колмогорова-Винера (7.4) в матричной форме будет

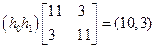или .

Отсюда получаем, что 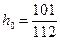и .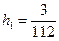

Обычно, чтобы не было усиления сигнала на выходе фильтра за счет свертки весовые коэффициенты нормируют путем .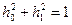

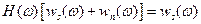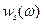Применяя к выражению (7.3) свойства преобразований Фурье о линейности и свертке, получаем частотную характеристику фильтра Колмогорова-Винера , а именно: , где и 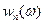- энергетические спектры сигнала и помех, рассчитанные по заданным АКФ, т.е.

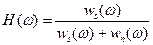(7.5).

Преимущества оптимального фильтра воспроизведения по сравнению с неоптимальными фильтрами сглаживания состоит в возможности получения оценок качества фильтрации. Для фильтра воспроизведения качество оценивается среднеквадратической погрешностью

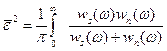(7.6).

Из последнего выражения следует, что если спектральная плотность помех мала по сравнению со спектральной интенсивностью сигнала, т.е. 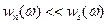, то 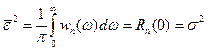, что означает равенство среднеквадратической погрешности сглаживания (воспроизведения) сигнала дисперсии помех .

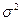Применение фильтра Колмогорова-Винера не ограничивается решением задач сглаживания, оно значительно шире. Поэтому ниже приводятся примеры использования фильтра для ряда часто встречающихся в практике обработки геофизических данных задач.