Построение фильтра прогнозирования.

На базе фильтра Колмогорова-Винера реализуется также построение фильтра прогнозирования для решения задачи прогноза или предсказания значений поля в «будущих», например, еще не измеренных, точках .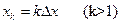

При этом для правой части уравнения (7.2) желаемым сигналом 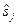является сам входной сигнал 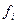, т.е. 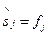в последующие моменты, например, времени, и взаимно корреляционная функция будет определена, как

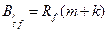(7.12)

Практическая реализация фильтра прогноза (7.12) сводится к многократному решению систем линейных уравнений для каждого заданного значения 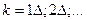Правая часть (7.12) при 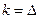представляет автокорреляционную функцию исходного поля без ее значения при m=0, при 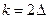- ту же АКФ без первых двух ее значений и т.д. После нахождения весовой функции для каждого значения k реализуется ее свертка с исходными значениями, что обеспечивает нахождение величины прогнозируемого значения поля. Фильтр прогнозирования предсказывает будущие значения сигнала по предшествующим значениям, т.е. «истории» входного сигнала и помехи. Следовательно, этот фильтр можно использовать и для решения задач интерполяции поля в любые наперед заданные точки.

На основе фильтра прогноза был построен новый метод оценки энергетических спектров, предложенный И.Бургом, отличающийся увеличением разрешающей способности по сравнению со спектрами Фурье. Однако дальнейшие его исследования позволили установить появление «ложных» экстремумов в спектре, не отвечающих реально наблюдаемым частотам.