Полиномиальная адаптивная фильтрация.

Рассмотрим еще один подход к построению линейных фильтров, ориентированных на повышение эффективности фильтрации нестационарных геофизических полей. Его суть состоит в комбинировании идей, описанных в предыдущих подразделах, и оригинального использования особенностей полиномиальных методов фильтрации.

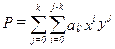Обычная полиномиальная фильтрация заключается в аппроксимации наблюдений полиномом в общем случае двух переменных - ой степени вида: - где 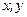‑ координаты точек сети наблюдения. Число членов такого полинома определяется выражением: .

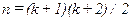Наиболее часто полиномиальная фильтрация применяется в задачах тренд-анализа, для оценки региональной (низкочастотной) составляющей поля. При этом степень полинома принимается равной единице, двум или трем, что соответствует аппроксимации исходных значений плоскостью, параболической или кубической поверхностью. Коэффициенты аппроксимирующего полинома находят с учетом значений поля во всех точках сети наблюдений.

Наиболее эффективно применение полиномиальной фильтрации в случаях, когда априори известно, что трендовая составляющая представлена полиномом определенной степени.

Рассмотрим алгоритм адаптивной полиномиальной фильтрации, учитывающей нестационарность поля по площади, посредством локализации оценок спектрально-корреляционных свойств поля и соответствующего изменения параметров фильтра (ширины, высоты, наклона и степени аппроксимирующего полинома). Блок схема такого алгоритма заключается в следующем.

Известно, что ориентация поверхности аппроксимирующего полинома обычно совпадает с корреляционным направлением исходного поля. Это делает несущественным такой параметр двумерного адаптивного фильтра, как текущий наклон 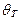окна фильтрации. Свойство аппроксимирующего полинома ориентироваться вдоль корреляционного направления в текущем окне, делает адаптивный полиномиальный фильтр более эффективным по сравнению с обычным двумерным адаптивным фильтром.

При полиномиальной фильтрации все точки внутри окна являются равноправными в отличие от других видов фильтраций, когда имеется одна исключительная точка, а именно центр окна, к которой и приписывается полученное в результате свертки профильтрованное значение поля. В связи с этим обстоятельством появляется возможность накопления информации, суть которого заключается в следующем. Каждая точка сети в процессе обработки попадает в некоторое множество окон, каждый раз получая очередное значение соответствующего полинома, равноправное со всеми другими. Результирующая величина в каждой точке, при таком накоплении, вычисляется как среднее значение из всех имеющихся в этой точке. Процесс накопления не эквивалентен увеличению размеров окна фильтра и не является рекурсией в чистом виде, поскольку значения поля из ближайшего окружения любой точки сети попадают в большее число окон по сравнению с удаленными точками и, следовательно, будут иметь больший вес. Таким образом, процесс накопления также изменяет параметры выходного сигнала в зависимости от свойств исходного поля в окружении конкретной точки.