Полиномиальная аппроксимация

Является одним из наиболее распространенных способов аппроксимации. Заключается в представлении нелинейной характеристики в виде полинома (многочлена) n-ой степени относительно рабочей точки (x₀, y₀):

,

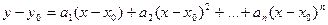где 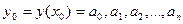- коэффициенты полинома. Зависят от положения рабочей точки на характеристике;

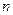- порядок полинома. Определяется требуемой точностью расчетов.

Примеры:

1) Полином второй степени:

-

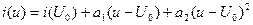- используется, если рабочая точка (определяется постоянным напряжением 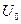) расположена на начальном участке характеристики, имеющем вид квадратичной параболы, и подводимое к НЭ напряжение сигнала не выходит за начало характеристики (за точку 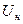, которая определяется из условия: i(U_н)=0).

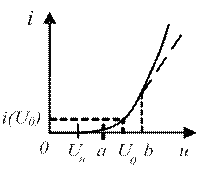
Рисунок 15.1 – Характеристика, для аппроксимации которой требуется полином второй степени. Используемые обозначения:

- i(U₀) – ток покоя;

- (a, b) – используемый участок ВАХ.

2) Неполный полином третьей степени:

-

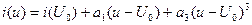- используется, если рабочая точка является точкой перегиба характеристики и напряжение сигнала не выходит за пределы напряжения насыщения +U_max.

Рисунок 15.2 – Характеристика, для аппроксимации которой требуется полином третьей степени.

3) Полином высокой (пятой и более) степени используется, если рабочая точка находится на нижнем сгибе характеристики и изменение напряжения сигнала велико.

Рисунок 15.3 – Характеристика, для аппроксимации которой требуется полином высокой степени.