Слабонелинейный режим работы НЭ

Рассмотрим режим работы, при котором напряжение сигнала 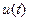не выходит за пределы точки начала характеристики 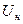(рисунок 15.1) и ВАХ удовлетворительно аппроксимируется степенным полиномом третьей степени:

,

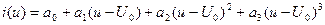где 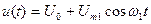- входной сигнал.

Подставим в заданный полином выражение входного сигнала:

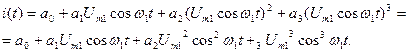
Применяя тригонометрические формулы кратных аргументов:

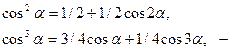
избавимся от степеней тригонометрических функций:

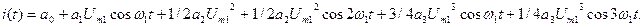
Сгруппируем слагаемые с одинаковым аргументом косинуса:

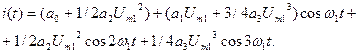
Заменим коэффициенты обозначением тока:

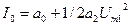- постоянная составляющая;

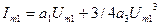- амплитуда первой гармоники;

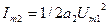- амплитуда второй гармоники;

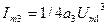- амплитуда третьей гармоники.

Отклик представим в виде:

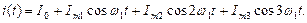
Представим воздействие и отклик графически.

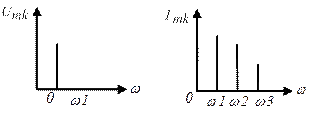
Рисунок 16.1 – Спектральные диаграммы гармонического воздействия и отклика на него.

Выводы:

- спектр отклика при воздействии гармонического сигнала линейчатый;

- частоты составляющих спектра кратны частоте входного сигнала;

- кратность частоты высшей гармоники спектра равна степени полинома;

- постоянная составляющая и четные гармоники определяются только четными степенями напряжения в полиноме;

- нечетные гармоники определяются только нечетными степенями напряжения в полиноме.

Отметим, что в спектре отклика появились составляющие, отсутствовавшие в спектре входного воздействия. Эти новые составляющие являются результатом реакции нелинейной цепи и называются нелинейными продуктами, характеризующими нелинейные искажения входного сигнала.

Рассмотренный метод используется при анализе работы усилителей, работающих в нелинейном режиме, т.е. когда допустим уровень нелинейных продуктов выше 10%.