Бигармоническое воздействие
Бигармоническое воздействие – это входной сигнал, представляющий собой сумму двух гармонических колебаний с разными частотами:
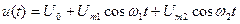 .
.
При анализе ограничимся третьей степенью аппроксимирующего полинома:
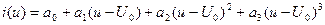 .
.
Подставим в заданный полином выражение входного сигнала:
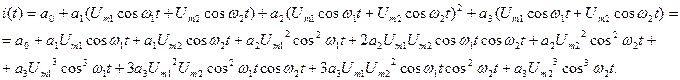 Применяя тригонометрические формулы кратных аргументов:
Применяя тригонометрические формулы кратных аргументов:
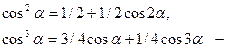
и произведения косинусов:
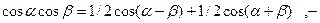
избавимся от спепеней и произведений тригонометрических функций:
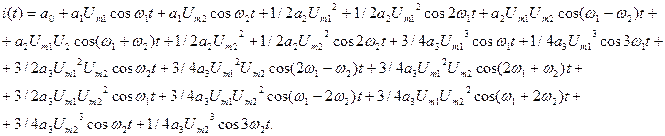
Сгруппируем слагаемые с одинаковым аргументом косинуса:
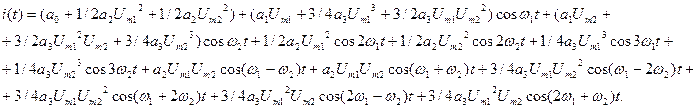 Заменим коэффициенты обозначением тока:
Заменим коэффициенты обозначением тока:
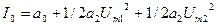 - постоянная составляющая;
- постоянная составляющая;
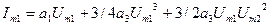 - амплитуда первой гармоники первой частоты;
- амплитуда первой гармоники первой частоты;
 - амплитуда первой гармоники второй частоты;
- амплитуда первой гармоники второй частоты;
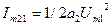 - амплитуда второй гармоники первой частоты;
- амплитуда второй гармоники первой частоты;
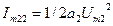 - амплитуда второй гармоники второй частоты;
- амплитуда второй гармоники второй частоты;
 - амплитуда третьей гармоники первой частоты;
- амплитуда третьей гармоники первой частоты;
 - амплитуда третьей гармоники второй частоты;
- амплитуда третьей гармоники второй частоты;
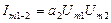 - амплитуда составляющей разностной частоты
- амплитуда составляющей разностной частоты 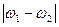 ;
;
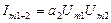 - амплитуда составляющей суммарной частоты
- амплитуда составляющей суммарной частоты 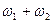 ;
;
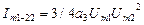 - амплитуда составляющей разностной частоты
- амплитуда составляющей разностной частоты 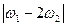 ;
;
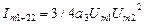 - амплитуда составляющей суммарной частоты
- амплитуда составляющей суммарной частоты 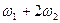 ;
;
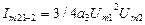 - амплитуда составляющей разностной частоты
- амплитуда составляющей разностной частоты 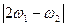 ;
;
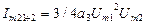 - амплитуда составляющей суммарной частоты
- амплитуда составляющей суммарной частоты 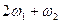 .
.
Отклик представим в виде:

Представим воздействие и отклик графически, предположив, что 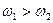 .
.
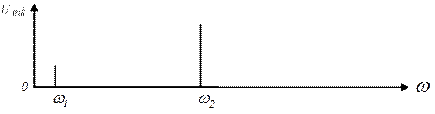
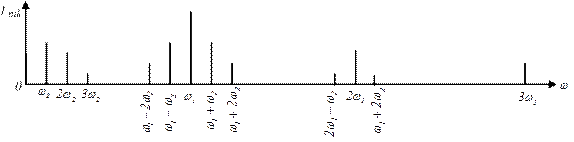
Рисунок 17.1 – Спектральные диаграммы бигармонического
воздействия и отклика на него.
Кроме постоянной составляющей и гармоник в составе тока появились комбинационные частоты - всевозможные суммарные и разностные частоты, не кратные частотам воздействия. Составляющие с такими частотами возникают только при одновременном воздействии на НЭ не менее двух гармонических колебаний.
Дата добавления: 2016-01-07; просмотров: 1840;
