Балансная и однополосная модуляции
Для более эффективного использования мощности спектра AM сигнала возможно исключение из спектра AM сигнала несущего колебания. Такой АМ сигнал называют балансно-модулированным (БМ). Также из спектра можно исключить одну боковую полосу частот (верхнюю или нижнюю), поскольку каждая из них содержит полную информацию о модулирующем сигнале 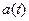 .При этом получается однополосную модуляцию(ОМ), т.е. модуляцию с одной боковой полосой — ОБП.
.При этом получается однополосную модуляцию(ОМ), т.е. модуляцию с одной боковой полосой — ОБП.
ЧАСТОТНАЯ МОДУЛЯЦИЯ
Угловая модуляция
Воздействие модулирующего сигнала 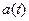 на аргумент (текущую фазу)
на аргумент (текущую фазу) 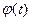 гармонической несущей
гармонической несущей 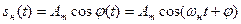 , называется угловой модуляцией (УМ). Разновидностями УМ являются частотная и фазовая.
, называется угловой модуляцией (УМ). Разновидностями УМ являются частотная и фазовая.
19.2 Частотная модуляция
Частотная модуляция (ЧМ) - процесс управления частотой гармонической несущей по закону модулирующего сигнала.
Угловая частота изменяется по закону:
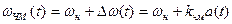 ,
,
где 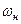 - частота несущей;
- частота несущей;
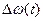 - отклонение частоты модулированного сигнала от значения
- отклонение частоты модулированного сигнала от значения 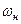 ;
;
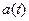 - модулирующий сигнал. Может быть гармоническим (используется для учебных или исследовательских целей) и негармоническим (реальный сигнал);
- модулирующий сигнал. Может быть гармоническим (используется для учебных или исследовательских целей) и негармоническим (реальный сигнал);
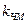 - размерный коэффициент пропорциональности, рад/(с∙В) или рад/(с∙А). Определяется схемотехникой модулятора.
- размерный коэффициент пропорциональности, рад/(с∙В) или рад/(с∙А). Определяется схемотехникой модулятора.
Полная фаза в момент времени t находится путем интегрирования частоты:
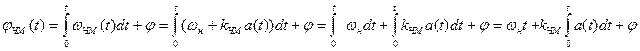 ,
,
где 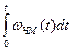 - набег фазы за время от начала отсчета до рассматриваемого момента
- набег фазы за время от начала отсчета до рассматриваемого момента 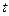 ;
;
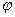 - постоянная интегрирования.
- постоянная интегрирования.
Математическая модель ЧМ сигнала:
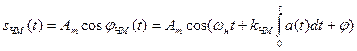 .
.
ЧМ называют интегральным видом модуляции, т.к. 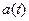 входит в это выражение под знаком интеграла.
входит в это выражение под знаком интеграла.
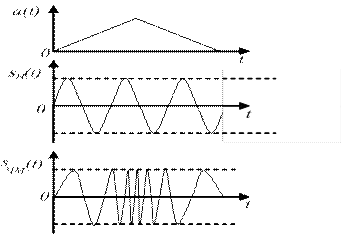
Рисунок 19.1 – Временные диаграммы модулирующего, несущего и
модулированного колебаний.
Гармоническая ЧМ
Рассмотрим гармоническую ЧМ (модулирующий сигнал является гармоническим 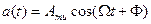 ).
).
Частота изменяется по закону:
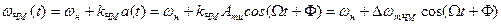 ,
,
где 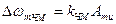 - девиация частоты при ЧМ. Девиация частоты – наибольшее отклонение частоты модулированного сигнала от значения частоты несущей. При ЧМ может принимать значения от единиц герц до сотен мегагерц.
- девиация частоты при ЧМ. Девиация частоты – наибольшее отклонение частоты модулированного сигнала от значения частоты несущей. При ЧМ может принимать значения от единиц герц до сотен мегагерц.
Фаза в момент времени 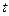 :
:
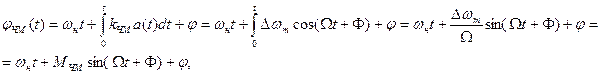
где 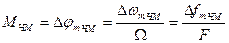 - индекс частотной модуляции. Является девиацией фазы при ЧМ. Девиация фазы - наибольшее отклонение фазы модулированного сигнала от линейной
- индекс частотной модуляции. Является девиацией фазы при ЧМ. Девиация фазы - наибольшее отклонение фазы модулированного сигнала от линейной 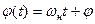 .
.
Математическая модель сигнала при гармонической ЧМ:
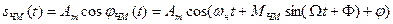 .
.
Воспользовавшись тригонометрической формулой: 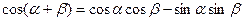 , - преобразуем выражение:
, - преобразуем выражение:
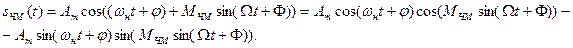
Проведем анализ отдельно для малых и больших индексов модуляции.
В первом случае ( 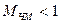 ) имеют место приближенные равенства:
) имеют место приближенные равенства:

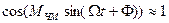 ,
, 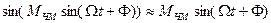 .
.
Воспользовавшись тригонометрической формулой: 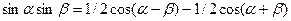 , -
, -
приходим к следующему выражению для ЧМ сигнала:
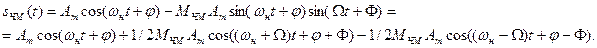

Рисунок 19.2 – Спектральная диаграмма ЧМ сигнала при МЧМ<1.
При малом индексе модуляции – узкополосной ЧМ – амплитудная спектральная диаграмма ЧМ сигнала совпадает по составу (содержит центральную составляющую с частотой несущей 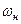 , нижнюю и верхнюю боковые составляющие с частотами
, нижнюю и верхнюю боковые составляющие с частотами 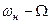 и
и 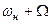 ) и ширине полосы частот (
) и ширине полосы частот ( 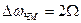 ) с АМ сигналом. Отличие заключается в фазовой спектральной диаграмме: фаза нижней боковой составляющей сдвинута на 1800.
) с АМ сигналом. Отличие заключается в фазовой спектральной диаграмме: фаза нижней боковой составляющей сдвинута на 1800.
При малом значении индекса модуляции не будут проявляться преимущества ЧМ (высокая помехозащищенность). Ширина спектра такая же, как и при АМ.
Во втором случае ( 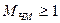 ) сложные периодические функции:
) сложные периодические функции: 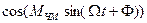 и
и 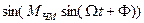 - можно разложить в ряд Фурье, а ЧМ сигнал представить в виде суммы гармонических колебаний:
- можно разложить в ряд Фурье, а ЧМ сигнал представить в виде суммы гармонических колебаний:
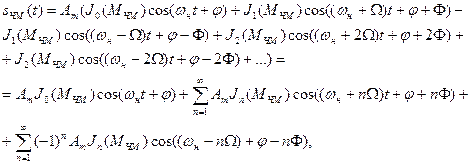
где 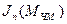 - функция Бесселя 1-го рода n-го порядка от вещественного аргумента
- функция Бесселя 1-го рода n-го порядка от вещественного аргумента 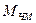 . Табулированы;
. Табулированы;
n – номер гармонической составляющей: центральная составляющая имеет n=0, боковые – n=1, 2, 3, … .

Рисунок 19.3 – Спектр ЧМ сигнала при МЧМ=2.
При большом индексе модуляции – широкополосной ЧМ – спектр ЧМ сигнала состоит из бесконечного числа гармоник: из составляющей с частотой несущей 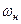 , нижней и верхней боковых полос частот, образованных группами составляющих с частотами
, нижней и верхней боковых полос частот, образованных группами составляющих с частотами 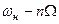 и
и 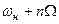 . На практике учитывают только те боковые составляющие, амплитуды которых не меньше 5% амплитуды несущей, т.е. для которых
. На практике учитывают только те боковые составляющие, амплитуды которых не меньше 5% амплитуды несущей, т.е. для которых 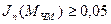 . Тогда ширина спектра ЧМ сигнала:
. Тогда ширина спектра ЧМ сигнала: 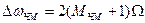 .
.
Данный случай представляет основной практический интерес, поскольку при больших индексах модуляции помехоустойчивость передачи сигнала существенно выше, чем при АМ. Ширина спектра ЧМ сигнала также значительно больше, чем при АМ.
При сложном модулирующем сигнале спектр модулированного сигнала оказывается сложным, содержащим различные комбинационные частоты. Общая полоса частот, занимаемая таким сигналом: 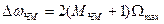 , где
, где 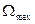 - максимальная частота спектра модулирующего сигнала;
- максимальная частота спектра модулирующего сигнала; 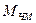 - индекс модуляции на этой частоте.
- индекс модуляции на этой частоте.
ФАЗОВАЯ МОДУЛЯЦИЯ
Фазовая модуляция
Фазовая модуляция (ФМ) – изменение фазы гармонической несущей по закону модулирующего сигнала.
Мгновенная фаза ФМ сигнала определяется выражением:
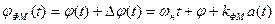 ,
,
где 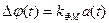 - отклонение (сдвиг) фазы модулированного сигнала от линейно-изменяющейся фазы гармонической несущей
- отклонение (сдвиг) фазы модулированного сигнала от линейно-изменяющейся фазы гармонической несущей 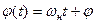 ;
;
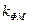 - размерный коэффициент пропорциональности, рад/В или рад/А.
- размерный коэффициент пропорциональности, рад/В или рад/А.
Математическая модель ФМ сигнала:
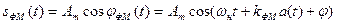 .
.
Угловая частота – это скорость изменения (т.е. производная по времени) полной фазы колебания. Выражение для мгновенной частоты:
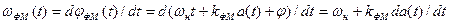 .
.
Таким образом, ФМ сигнал с модулирующим сигналом 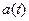 можно рассматривать как ЧМ сигнал с модулирующим сигналом
можно рассматривать как ЧМ сигнал с модулирующим сигналом 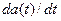 .
.

Рисунок 20.1 – Модулирующий сигнал, несущее колебание, изменение фазы ФМ сигнала, изменение частоты ФМ сигнала и ФМ сигнал.
Гармоническая ФМ
Рассмотрим случай гармонического модулирующего сигнала:
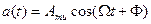 .
.
Фаза сигнала с гармонической ФМ:
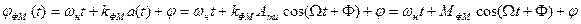 ,
,
где 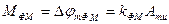 - индекс фазовой модуляции или девиация фазы при ФМ. Может принимать значение от единиц до десятков тысяч радиан.
- индекс фазовой модуляции или девиация фазы при ФМ. Может принимать значение от единиц до десятков тысяч радиан.
Математическая модель сигнала с гармонической ФМ:
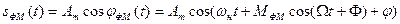 .
.
Частота ФМ сигнала:
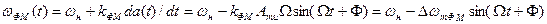 ,
,
где 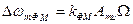 - девиация частоты при ФМ.
- девиация частоты при ФМ.
Методология вычисления и структура спектра ФМ сигнала аналогичны ЧМ сигналу, но индекс частотной модуляции необходимо заменить индексом фазовой модуляции. Аналогичная тесная связь между спектрами ФМ и ЧМ сигналов имеет место и при негармонических модулирующих сигналах.
ФМ применяется в схемах косвенного метода получения ЧМ.
МАНИПУЛЯЦИЯ
Виды манипуляции
дискретная модуляция (манипуляция) - модуляция гармонического несущего колебания дискретным (цифровым) модулирующим сигналом. При этом модулируемые (информационные) параметры переносчика изменяются скачкообразно. Устройство, реализующее процесс манипуляции, называют манипулятором.
Дискретным модулирующим сигналом является первичный сигнал, отображающий символы кодовых комбинаций дискретных сообщений. Примеры дискретных первичных сигналов: телеграфный, передачи данных, ИКМ.
Различают следующие виды манипуляции:
- в зависимости от изменяемых параметров переносчика:
- амплитудную (АМн; английский термин – amplitude shift keying, ASK),
- частотную (ЧМн; английский термин – frequency shift keying, FSK),
- фазовую (ФМн; английский термин – phase shift keying, PSK),
- амплитудно-фазовую (АФМн; английский термин – APK/PSK, или amplitude phase keying, APK).
При АМн каждому возможному значению передаваемого символа ставится в соответствие своя амплитуда гармонического несущего колебания, при ЧМн – частота, при ФМн – фаза, а при АФМн – комбинация амплитуды и начальной фазы;
- в зависимости от используемых кодов:
- многопозиционную или 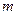 -арную (по-английски – m-ary),
-арную (по-английски – m-ary),
- двоичную (по-английски – binary).
Многопозиционная манипуляция используется для повышения скорости передачи информации при одной и той же скорости модуляции. 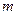 - основание многопозиционного кода – число различных его символов. На практике обычно является ненулевой степенью двойки:
- основание многопозиционного кода – число различных его символов. На практике обычно является ненулевой степенью двойки: 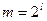 , где
, где 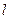 - число двоичных цифр (битов), представляющих символы многопозиционного кода. Двоичная манипуляция (
- число двоичных цифр (битов), представляющих символы многопозиционного кода. Двоичная манипуляция ( 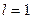 ,
, 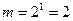 ) является частным случаем многопозиционной. Как правило, в системах передачи дискретных сообщений используются двоичные коды.
) является частным случаем многопозиционной. Как правило, в системах передачи дискретных сообщений используются двоичные коды.
Двоичная АМн
При двоичном коде первичный сигнал принимает два значения, соответствующие кодовым символам 0 и 1:
- (-Umи, Umи) – двухполярный сигнал;
- (0, Umи) – однополярный сигнал.
При двоичной АМн (BASK) символу 1 соответствует отрезок гармонического несущего колебания (посылка), символу 0 – отсутствие колебания (пауза), поэтому часто АМн называют манипуляцией с пассивной паузой.
Примем в качестве модулирующего меандровый сигнал – сигнал, отображающий последовательность битов повторяющегося двоичного кода 1010.

Рисунок 21.1 – Временные диаграммы модулирующего и АМн сигналов.
АМн можно рассматривать как модуляцию сигналом со спектром, богатым гармониками: спектр меандрового сигнала содержит бесконечное количество нечетных гармоник. Спектр АМн сигнала содержит составляющую с частотой несущей и две боковые полосы, каждая из которых повторяет спектр первичного сигнала.

Рисунок 21.2 – Спектральные диаграммы модулирующего и АМн сигналов.
Теоретически спектр сигнала при АМн бесконечен. На практике бесконечный спектр ограничивается полосой пропускания фильтра. Соотношение для расчета ширины спектра АМн сигнала:
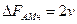 ,
,
где 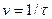 - символьная скорость или скорость модуляции, Бод – число символов кода, передаваемых за единицу времени (1 с);
- символьная скорость или скорость модуляции, Бод – число символов кода, передаваемых за единицу времени (1 с);
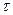 - символьный (тактовый) интервал – интервал времени, отведенный для передачи одного символа.
- символьный (тактовый) интервал – интервал времени, отведенный для передачи одного символа.
АМн была изобретена в начале 20 столетия для беспроводной телеграфии. В настоящее время АМн в системах цифровой связи уже не используется.
Двоичная ЧМн
При двоичной ЧМн (BFSK) символу 1 соответствует отрезок гармонического колебания с частотой 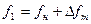 , а символу 0 – с частотой
, а символу 0 – с частотой 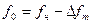 , где
, где 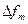 - девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения
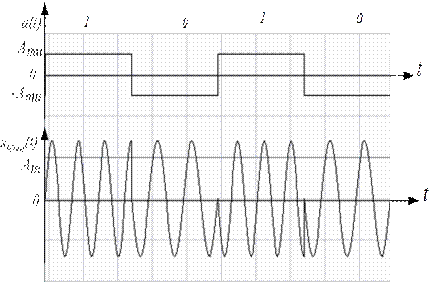
- девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения 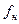 . При ЧМн нет пассивной паузы, по этой причине ее называют манипуляцией с активной паузой.
. При ЧМн нет пассивной паузы, по этой причине ее называют манипуляцией с активной паузой.
Возможно два случая ЧМн: с разрывом фазы и без разрыва фазы (continuous-phase FSK – CPFSK).
При ЧМн с разрывом фазы назначение каждому двоичному символу своей частоты является произвольным. Полученный сигнал содержит скачки фазы.
|
|
Наличие разрывов фазы приводит к «размытию» спектра сигнала. Это снижает помехоустойчивость приема и создает помехи другим системам связи. Поэтому при выборе частот следует обеспечить условие плавного (без скачка фазы) перехода от сигнала с частотой 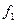 к сигналу с частотой
к сигналу с частотой 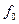 :
:
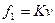 и
и 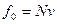 ,
,
где 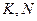 - число периодов внутри символьного интервала.
- число периодов внутри символьного интервала.
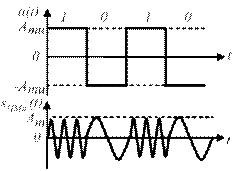
Рисунок 21.4 – Временные диаграммы сигналов: модулирующего и ЧМн
без разрыва фазы.
ЧМн сигнал можно рассматривать как сумму двух отдельных АМн сигналов, один из которых служит только для отображения единиц и имеет несущую частоту 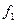 , а другой – только нулей и имеет несущую частоту
, а другой – только нулей и имеет несущую частоту 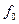 . Соответственно, спектр ЧМн сигнала может быть представлен как суперпозиция спектров двух АМн сигналов.
. Соответственно, спектр ЧМн сигнала может быть представлен как суперпозиция спектров двух АМн сигналов.

Рисунок 21.5 – Спектральная диаграмма ЧМн сигнала.
Ширина спектра сигнала с двоичной ЧМн определяется выражением:
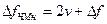 ,
,
где 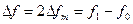 - разнос частот – расстояние между частотами
- разнос частот – расстояние между частотами 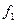 и
и 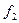 . Выбирается таким, чтобы не перекрывались спектры отдельных АМн сигналов;
. Выбирается таким, чтобы не перекрывались спектры отдельных АМн сигналов;
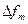 - девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения
- девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения 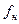 .
.
ЧМн применяется в радиорелейных и спутниковых системах связи, системах связи с подвижными объектами.
Двоичная ФМн
Различают абсолютную ФМн и относительную ФМн (ОФМн; differential PSK – DPSK).
При ФМн информация вкладывается в абсолютное значение фазы сигнала, т.е. смещение фазы модулированного сигнала относительно фазы несущего колебания. При ОФМн фазу сигнала отсчитывают от фазы предыдущего элемента сигнала.
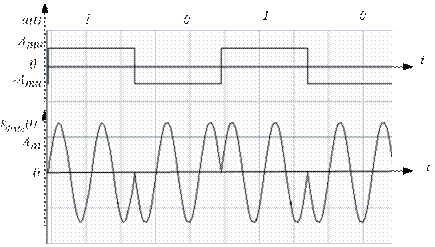
При двоичной ФМн (BPSK) передаче 1 соответствует отрезок гармонического колебания, совпадающего по фазе с несущей, а передаче 0 - отличающегося по фазе на 180°, т.е. фаза меняется на 180° при каждом переходе от 1 к 0 и наоборот.
|
 Рисунок 21.6 – Временная диаграмма модулирующего и ФМн сигналов.
Рисунок 21.6 – Временная диаграмма модулирующего и ФМн сигналов.
ФМн сигнал можно представить в виде суммы двух АМн сигналов, для получения первого из которых используется несущая 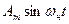 , а второго -
, а второго - 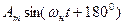 . Спектр амплитуд ФМн сигнала содержит те же составляющие, что и спектр АМн сигнала, кроме составляющей с частотой несущей (она исчезает, когда символы 1 и 0 появляются с равной вероятностью). Амплитуды боковых составляющих примерно в два раза больше. При передаче реальных кодовых слов амплитуда составляющей с частотой несущей не равна нулю, но будет значительно ослаблена.
. Спектр амплитуд ФМн сигнала содержит те же составляющие, что и спектр АМн сигнала, кроме составляющей с частотой несущей (она исчезает, когда символы 1 и 0 появляются с равной вероятностью). Амплитуды боковых составляющих примерно в два раза больше. При передаче реальных кодовых слов амплитуда составляющей с частотой несущей не равна нулю, но будет значительно ослаблена.

Рисунок 21.6 – Спектр ФМн сигнала.
При ОФМн символ 0 передается отрезком гармонического колебания с начальной фазой предшествующего элемента сигнала, а символ 1 – таким же отрезком с начальной фазой, отличающейся от начальной фазы предшествующего элемента на 180° (фаза изменяется при передаче символов 1), или наоборот (фаза изменяется при передаче символов 0). При ОФМн передача начинается с посылки одного не несущего информации элемента, который служит опорным сигналом для сравнения фазы последующего элемента.
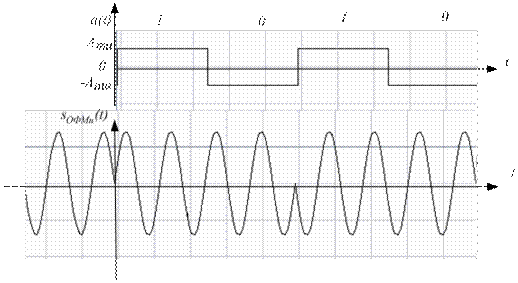
Рисунок 21.7 – Временная диаграмма модулирующего и ОФМн сигнала.
Спектр ОФМн сигнала подобен спектру ФМн сигнала.
ФМн сигнал имеет такую же полосу частот, как АМн сигнал:
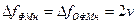 .
.
ФМн была разработана в начале развития программы исследования дальнего космоса и сейчас широко используется в коммерческих и военных системах связи.
Дата добавления: 2016-01-07; просмотров: 4589;
