Существенно нелинейный режим работы НЭ
Рассмотрим режим работы, получаемый при сдвиге рабочей точки 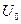 влево и увеличении амплитуды возбуждающего напряжения (рисунок 15.4). В данном случае целесообразно применить кусочно-линейную аппроксимацию ВАХ:
влево и увеличении амплитуды возбуждающего напряжения (рисунок 15.4). В данном случае целесообразно применить кусочно-линейную аппроксимацию ВАХ:
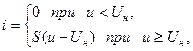
где 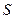 - крутизна линейно возрастающего участка ВАХ,
- крутизна линейно возрастающего участка ВАХ,
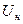 - координата его начала.
- координата его начала.
Форму реакции находим графическим методом. Типичное взаимное расположение ВАХ и сигналов показано на рисунке 16.2.

Рисунок 16.2 – Определение формы реакции методом проекций.
Форма реакции имеет вид периодической последовательности косинусоидальных импульсов с отсечкой. Полученные импульсы характеризуются двумя параметрами: высотой  и шириной
и шириной 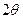 .
.
Угол, соответствующий половине времени существования импульса, называется углом отсечки 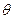 . Угол отсечки определяется из равенства:
. Угол отсечки определяется из равенства:
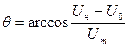 .
.
В соответствии с формулой при заданной ВАХ (фиксированном 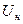 ) угол отсечки
) угол отсечки 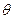 регулируется выбором амплитуды
регулируется выбором амплитуды 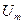 величины смещения
величины смещения 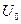 .
.
Высота (максимальное значение) импульса тока определяется выражением:
 .
.
Поскольку ток – периодическая функция времени с периодом 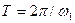 , его можно представить в виде ряда Фурье:
, его можно представить в виде ряда Фурье:
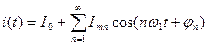 .
.
Коэффициенты этого ряда являются постоянной составляющей и амплитудами гармоник тока и могут быть вычислены по формулам:
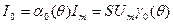 ,
,
 ,
,
где 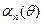 - коэффициенты Берга;
- коэффициенты Берга;
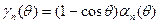 - функции Берга.
- функции Берга.
Для ряда значений 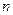 коэффициенты и функции Берга табулированы.
коэффициенты и функции Берга табулированы.
Из рассмотрения графиков коэффициентов Берга можно сделать такие заключения: при 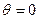 ток равен нулю (НЭ заперт на протяжении всего периода); при
ток равен нулю (НЭ заперт на протяжении всего периода); при 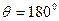 отсечка тока отсутствует и режим работы становится линейным; при работе с
отсечка тока отсутствует и режим работы становится линейным; при работе с 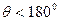 отношение амплитуды первой гармоники к постоянной составляющей больше единицы
отношение амплитуды первой гармоники к постоянной составляющей больше единицы 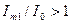 и растет с уменьшением
и растет с уменьшением 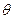 ; с повышением номера гармоники максимумы амплитуд гармоник перемещаются в область малых значений
; с повышением номера гармоники максимумы амплитуд гармоник перемещаются в область малых значений 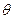 .
.
Указанные обстоятельства существенно влияют на выбор режима работы НЭ при усилении колебаний, умножении частоты. При умножении частоты для получения наибольшей амплитуды нужной гармоники тока ( 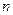 -ой) необходимо выбрать оптимальное значение угла отсечки:
-ой) необходимо выбрать оптимальное значение угла отсечки:
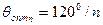 .
.
Таким образом, вне зависимости от вида аппроксимирующей функции ток через НЭ при гармоническом воздействии представляется суммой постоянной 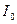 и гармонических с амплитудами
и гармонических с амплитудами 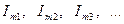 и частотами
и частотами  , кратными частоте приложенного напряжения, составляющих, т.е. рядом Фурье.
, кратными частоте приложенного напряжения, составляющих, т.е. рядом Фурье.
Дата добавления: 2016-01-07; просмотров: 1179;
