Временная стоимость денег
Понятие «временная стоимость денег» - относительно новое для отечественной теории и практики. Между тем, во всем цивилизованном мире расчеты, связанные с определением «будущей стоимости денег», «текущей (настоящей) стоимости денег» стали уже традиционными. Они позволяют со значительной долей вероятности прогнозировать в каждом конкретном случае финансовые результаты от вложения денег в тот или иной проект.
В основе концепции временной стоимости денег лежат положения о том, что, во-первых, деньги с течением времени всегда меняют свою стоимость; во-вторых, «сегодняшние» деньги всегда дороже тех, которые будут получены нами завтра.
При этом, концепция временной стоимости денег абстрагируется от инфляционного фактора, а привлекательность «сегодняшних» денег объясняется тем, что последние всегда можно инвестировать с целью получения в будущем большего дохода.
Будущая стоимость денег – это стоимость наших «сегодняшних» денег с учетом полученного на них дохода в будущем, на определенную дату.
Расчет будущей стоимости денег осуществляется по принципу сложного процента, механизм действия которого состоит в том, что процент начисляется и на основную часть денежного вклада и на полученные ранее проценты.
Общепринятая формула сложного процента для расчета будущей стоимости денег выглядит следующим образом:
Fn = Ф(1+i)n
Где: Fn – будущая сумма денег, получаемая в конце расчетного периода;
Ф – первоначальное вложение денег;
i – процентная ставка доходности вложений;
n – срок, на который делается вложение (расчетный период)
Рассмотрим исчисление (расчет) будущей стоимости денег на следующем примере.
Пример 1. Допустим акционерное общество «Гамма» заключило договоры на открытие депозитных счетов с коммерческими банками А и Б. Оба счета открыты на 100 млн рублей, сроком на два года, с выплатой процента в размере 144 % годовых. При этом, банк А выплачивает проценты ежеквартально, а банк Б – ежемесячно. Какую же сумму будет иметь АО «Гамма» по окончании 2-х летнего периода на каждом из счетов?
Расчет: Банк А: 1) Вложенная сумма – 100 млн рублей; 2) количество выплатных периодов – по 4 раза каждый год, итого 8 раз; 3)процентная ставка каждого конкретного начисления – 144 : 4 = 36 %. Используя формулу сложного процента получаем:
Fn = 100 млн руб. х (1+0,36)8 = 100 х 11,703 = 1170,3 млн руб.
Банк Б: 1) Вложенная сумма – 100 млн рублей; 2) количество выплатных периодов – по 12 каждый год, итого 24 раза; 3) Процентная ставка каждого конкретного начисления – 144 : 12 = 12 %. Используя формулу сложного процента, получаем:
100 млн руб. х (1+0,12)24 = 100х15,179 = 1517,9 млн руб.
Итак, расчет будущей стоимости денег позволяет не только рассчитать вероятную доходность вложений, но и выбрать наиболее предпочтительный вариант размещения «сегодняшних» денег.
Текущая (настоящая) стоимость денег – это стоимость «завтрашних» денег сегодня. Рассчитывая текущую стоимость денег мы можем определить реальную стоимость отсроченного платежа или выбрать наиболее эффективный вариант вложения денежных средств, из имеющихся. Расчет текущей стоимости денег обратно пропорционален формуле сложного процента для исчисления будущей стоимости денег и выглядит следующим образом:
Ф=Fn 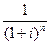 ;
;
где: Ф – первоначально вкладываемая сумма денег для осуществления инвестиционного проекта;
Fn – сумма денег, полученная в результате реализации инвестиционного проекта;
I – процентная ставка дохода по основному или альтернативному варианту (депозитный процент) вложения средств;
n – период реализации инвестиционного проекта.
Рассчитаем текущую стоимость денег, исходя из следующих двух примеров.
Пример 2. Акционерное общество «Гамма» приглашено для участия в реализации инвестиционного проекта, реализация которого должна обеспечить через 2 года получение дохода в сумме 100 млн. руб. Процентная ставка по депозитам в текущем периоде составляет 144 % с выплатой 4 раза в год. Необходимо определить настоящую стоимость прогнозируемых доходов в сумме 100 млн. руб.
Расчет: 1) Планируемая сумма дохода – 100 млн. руб. 2) Средняя депозитная ставка в текущем периоде 144 %, с учетом четырех выплат в течение года – 36 %; 3) Частота выплаты депозитного процента за рассматриваемый период – 8 раз. Используя формулу определения текущей стоимости денег, получаем:
Ф = 100 млн. руб. х  = 100 млн.. руб. х
= 100 млн.. руб. х 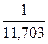 = 100 млн. руб. х 0,0854 = 8,54 млн. руб.
= 100 млн. руб. х 0,0854 = 8,54 млн. руб.
Таким образом, участие в проекте будет эффективным, если первоначальная сумма вложений не превысит 8, 54 млн. руб.
Пример 3. Акционерное общество «Гамма» планирует реализовать инвестиционный проект общей стоимостью 400 млн. руб. и продолжительностью 21 месяц. В ходе его реализации прогнозируется получение дохода в следующих размерах:
Первые 9 месяцев – 390 млн. руб.;
Следующие 6 месяцев – 650 млн. руб.;
Последующие 6 месяцев – 300 млн. руб.
Средняя депозитная ставка текущего периода составляет 36% за квартал.
Расчет: 1) Вложение 400 млн. руб. в банк на депозит за 21 месяц (9 мес. + 6 мес. + 6 мес.) принесет (по формуле сложного процента):
Fn = 400 млн. руб. х (1+0,36)7 = 400 млн. руб. х 8,6054=3442,16 млн. руб.
2) Вложение первого дохода в сумме 390 млн. руб. в банк на депозит на период 12 месяцев принесет:
Fn = 390 млн. руб. х (1+0,36)4 = 390 млн. руб. х 3,4210=1334,19 млн. руб.
3) Вложение дохода второго периода в сумме 650 млн. руб. в банк на депозит на период в 6 месяцев принесет:
Fn = 650 млн руб. х (1+0,36)2 = 650 млн. руб. х 1,8494 = 1202,24 млн. руб.
4) Определяем будущую стоимость доходов после реализации инвестиционного проекта:
Млн. руб.
5) Определяем текущую (настоящую) стоимость получаемой к концу 21 месяца суммы по формуле расчета текущей стоимости денег:
Ф = 2836,43 х 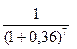 = 2836,43 х
= 2836,43 х 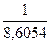 = 2836,43х0,1162 = 329,6
= 2836,43х0,1162 = 329,6
Таким образом, очевидно, что реализация данного инвестиционного проекта неэффективена по сравнению с простым размещением средств на депозит в банке.
То, что в вышеприведенных расчетах не принимается во внимание уровень инфляции, это не влияет на корректность выводов. Дело в том, что абсолютные суммы доходов будущих периодов рассчитываются с позиции сегодняшнего дня и сравниваются с сегодняшними вложениями. Этот паритет и обеспечивает справедливость сделанных расчетов.
Тема: Денежная система: ее основные типы и элементы
Дата добавления: 2015-11-28; просмотров: 1207;
