Многомерные аналоги метода обратных вероятностей и самонастраивающейся фильтрации.

В данном разделе рассматриваются методы обнаружения слабых многопризнаковых геофизических аномалий, которые являются многомерными аналогами способов обратных вероятностей и самонастраивающейся фильтрации. Слабыми многопризнаковыми аномалиями будем называть такие аномалии, энергетическое отношение которых

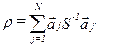(8.21)

меньше единицы. Здесь N - число аномальных точек, 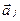- значения многопризнаковой аномалии и 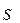- оценка ковариационной матрицы по значениям многопризнаковой аномалии. Отдельные компоненты таких аномалий по отдельным признакам практически не выделяются визуально, и их амплитуда соизмерима или меньше уровня осложняющих аномальные эффекты помех.

8.7.1.Многомерный способ обратных вероятностей.

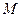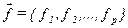Математическая модель многомерного аналога способа обратных вероятностей состоит в следующем. Пусть имеется сеть наблюдений размером в профилей и пикетов. В каждой точке наблюдения значения представлены вектором , отдельные компоненты которого являются значения по различным геофизическим полям или их трансформантам (признакам). Считается, что наблюдения в отдельной 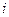‑ ой точке представлены либо суммой многопризнаковой аномалии 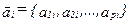и помехи 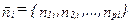. т.е. 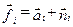. либо только помехой, т.е. 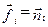. На векторную помеху накладывается условие о ее 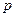‑мерном нормальном распределении с нулевым вектором среднего и ковариационной матрицей .

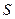Кроме того, предполагается некоррелированный характер помехи каждого из признаков по площади наблюдений. Как и в одномерном случае, для построения алгоритма обработки необходима априорная информация о параметрах многопризнаковой аномалии и о величине дисперсии помехи по каждому признаку.

На основе описанной модели наблюдений, задача обнаружения 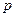‑мерной многопризнаковой аномалии формулируется следующим образом: для имеющейся последовательности многопризнаковых наблюдений 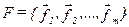, требуется определить, являются ли наблюдения суммой известной по форме многопризнаковой аномалии (заданной в 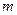точках) и 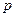‑мерной помехи (гипотеза 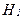), или же эти наблюдения представлены лишь помехой по каждому из признаков (гипотеза ).

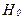По аналогии с одномерным вариантом способа обратных вероятностей формула 8.14. для расчета коэффициента правдоподобия 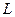и проверки гипотезы 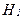будет иметь вид:

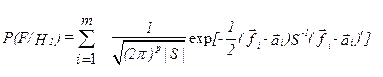(8.22)

соответственно для нулевой гипотезы :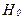

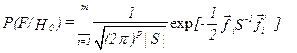(8.23)

Коэффициент правдоподобия в этом случае равен:

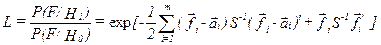
Поскольку ковариационная матрица помехи симметрична, то справедливы следующие преобразования:

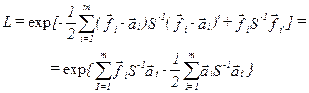
Согласно критерию максимального правдоподобия при выполнении неравенства 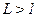будет справедлива гипотеза 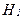. в противном случае справедлива гипотеза 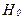. Выполнение неравенства 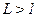эквивалентно выполнению неравенства:

Переход от коэффициента правдоподобия к апостериорной вероятности наличия аномалии осуществляется по формуле Байеса.

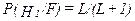
При 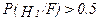принимается решение о наличии многопризнаковой аномали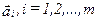и , при 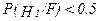‑ об ее отсутствии. Надежность обнаружения аномалии определяется через интеграл вероятности по аналогии с одномерным случаем с использованием величины 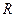из (8.21):