Метод динамических сгущений (k-средних).

Достаточно известный и эффективный метод классификации многомерных наблюдений на заранее известное число классов 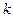в условиях минимума информации о начальных центрах классов, известный под названием k-средних или k-ближайших соседей. Блок схема алгоритма заключается в следующем:

-для всех 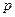обрабатываемых признаков оценивается значение среднеквадратического отклонения 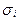, минимального 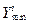и максимального 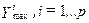значений;

-каждый 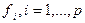признак нормируется на соответствующее значение среднеквадратического отклонения ;

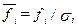-случайным образом выбирается 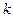векторов размерности 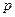начальных центров классов 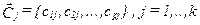. причем отдельные случайно выбранные компоненты каждого вектора удовлетворяют неравенству ;

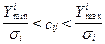-осуществляется классификация нормированных многопризнаковых наблюдений исходной сети на классы, при этом значение в каждой точке сети 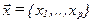относится к классу 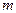. если расстояние от центра этого класса до точки является минимальным ;

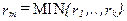-по результатам классификации определяются новые вектора центров классов. 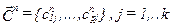. при этом каждая компонента отдельного вектора 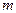является оценкой среднего 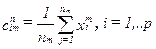. рассчитанной по 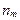точкам, попавшим в класс 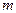после классификации. проведенной на предыдущем шаге алгоритма;

-в выбранной метрике оцениваются расстояния между старыми и новыми центрами классов ;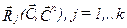

-если хотя бы для одного из 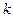классов расстояние больше заранее выбранной величины 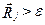. то старым векторам центров классов присваиваются значения новых 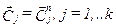и процедура повторяется с шага, на котором осуществляется классификации наблюдений. В противном случае, когда для всех классов выполняется неравенство 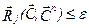, результаты последней итерации считаются окончательными.

Рассмотренный итерационный алгоритм обладает довольно быстрой сходимостью. Основным его недостатком является недостаточный учет корреляционных связей признакового пространства и необходимость задания конечного числа классов.

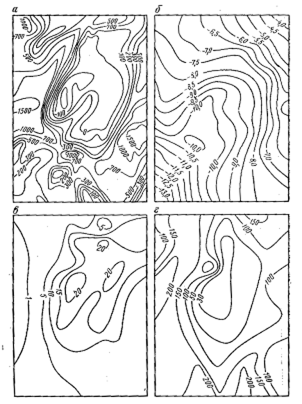
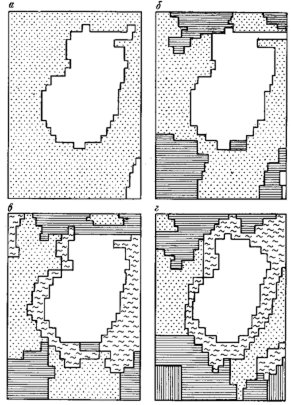
Рис.9.1.Геофизические поля над Бенкалинским меднопорфировым месторождением: а) Za в nT, б) ∆g в mG, в) - hk в %, г) rk в Ом×м.	Рис.9.2.Результат классификации геофизических полей методом к-средних на два а), три б), четыре в) и пять г) классов.